Vrijheidsgraden (Degrees of Freedom) | Definitie & Formules
Vrijheidsgraden (degrees of freedom), meestal aangeduid met df of 
, is het aantal onafhankelijke stukjes informatie dat wordt gebruikt om een statistiek te berekenen. Je berekent de vrijheidsgraden door het aantal beperkingen van de steekproefgrootte af te halen.
Vrijheidsgraden worden normaal gesproken tussen haakjes naast de teststatistiek vermeld, samen met de resultaten van de statistische test.
De teststatistiek, t, heeft 9 vrijheidsgraden, want:
df = n – 1 (waarbij n = de steekproefgrootte)
df = 10 – 1
df = 9
Je berekent een t-waarde van 1.41 voor de steekproef, wat overeenkomt met een p-waarde van .19. Je rapporteert je resultaten:
“De gemiddelde dagelijkse calciuminname van de deelnemers verschilde niet van de aanbevolen hoeveelheid van 1000 mg, t(9) = 1.41, p = 0.19.”
Wat zijn vrijheidsgraden?
Bij inferentiële statistiek schat je een parameter van een populatie door een statistiek van een steekproef te berekenen. De onafhankelijke stukjes informatie die gebruikt worden om de statistiek te berekenen worden de vrijheidsgraden genoemd. De vrijheidsgraden van een statistiek hangen af van de steekproefgrootte:
- Als de steekproefgrootte klein is, zijn er maar een paar onafhankelijke stukjes informatie, en dus maar een paar vrijheidsgraden.
- Als de steekproefgrootte groot is, zijn er veel onafhankelijke stukjes informatie, en dus veel vrijheidsgraden.
Als je een parameter schat, moet je beperkingen (restrictions) invoeren in de manier waarop de waarden aan elkaar gerelateerd zijn. Hierdoor zijn de stukjes informatie niet allemaal onafhankelijk. Met andere woorden: niet alle waarden in de steekproef zijn vrij om te variëren.
De volgende analogie en het volgende voorbeeld laten zien wat het betekent als een waarde vrij kan variëren en hoe de introductie van beperkingen hier invloed op heeft.
Vrij om te variëren: Analogie
Door elke dag een ander toetje te nemen, legt je kamergenote een beperking op aan haar toetjeskeuze.
Op maandag is ze vrij om uit alle zeven toetjes te kiezen. Op dinsdag kan ze kiezen uit één van de zes overgebleven opties. Op woensdag mag ze nog uit één van de vijf overgebleven opties kiezen, enzovoorts.
Op zondag heeft ze alle toetjes gehad, op één na. Ze heeft geen keuze op zondag, omdat er nog maar één optie over is.
Door haar beperking kon je kamergenote maar op zes van de zeven dagen haar toetje kiezen. Haar toetjeskeuze was vrij om te variëren op deze zes dagen. Daarentegen was haar toetjeskeuze op de laatste dag niet vrij om te variëren. De zevende keuze hing af van haar keuzes van de zes voorafgaande dagen.
Vrij om te variëren: Voorbeeld met rekensom
Voor het eerste getal kun je elk geheel getal kiezen dat je wilt. Wat je keuze ook is, de som van de vijf getallen kan nog steeds 100 zijn. Dit geldt ook voor het tweede, derde en vierde getal.
Voor het laatste getal heb je geen keuze. Het vijfde getal heeft slechts één mogelijke waarde en is niet vrij om te variëren.
Bijvoorbeeld: als je voor de eerste vier getallen 15, 27, 42 en 3 kiest, moet het laatste getal 13 zijn om tot een som van 100 te komen.
Door deze beperking kon je slechts vier van de vijf getallen kiezen. De eerste vier getallen waren vrij om te variëren. Het vijfde getal was niet vrij om te variëren, maar hing af van de eerste vier getallen.
Vrijheidsgraden en hypothesetoetsing
De vrijheidsgraden van een teststatistiek bepalen de kritieke waarde van de hypothesetoets. De kritieke waarde wordt berekend op basis van de nulverdeling en is een grenswaarde om te beslissen of de nulhypothese moet worden verworpen.
De vrijheidsgraden beïnvloeden de kritieke waarde door de vorm van de nulverdeling te veranderen. De nulverdelingen van de t-toets, chi-kwadraattoets en andere teststatistieken veranderen door de vrijheidsgraden, maar ieder op een andere manier.
t-toets
Om een t-toets uit te voeren, bereken je de t-waarde voor een steekproef en vergelijk je deze waarde met de kritieke waarde. Om de juiste kritieke waarde te vinden, moet je (Student’s) t-verdeling gebruiken met de juiste vrijheidsgraden.
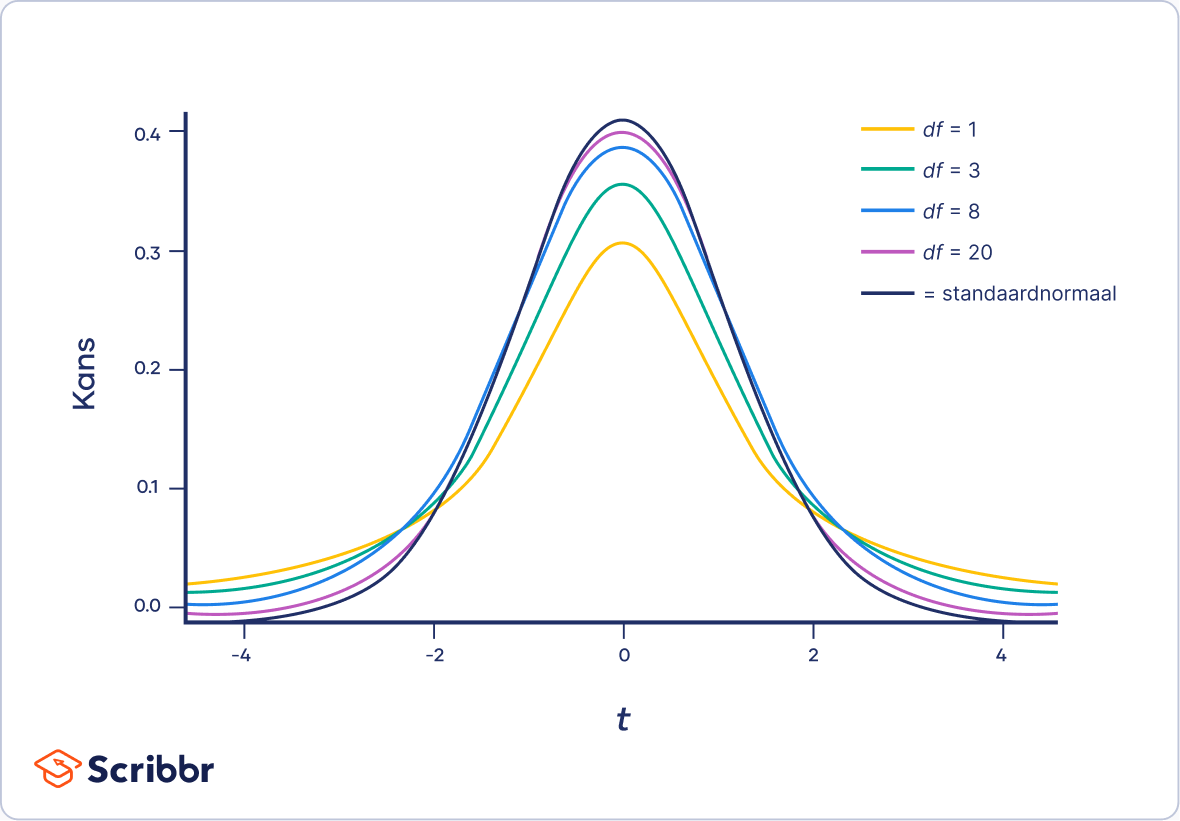
De nulverdeling van de t-toets verandert met het aantal vrijheidsgraden:
- Als df = 1, dan is de verdeling sterk leptokurtisch, wat betekent dat de kans op extreme waarden groter is dan bij een normale verdeling.
- Naarmate het aantal df toeneemt, wordt de verdeling smaller en minder leptokurtisch. De verdeling gaat dan meer lijken op een standaardnormale verdeling.
- Als df ≥ 30, dan is de verdeling bijna gelijk aan een standaardnormale verdeling. Als je een steekproefgrootte hebt van meer dan 30, kun je de standaardnormale verdeling (ook wel bekend als de z-verdeling) gebruiken in plaats van een t-verdeling.
Deze verandering in de vorm van de verdeling is logisch te begrijpen. De t-verdeling heeft minder spreiding naarmate het aantal vrijheidsgraden toeneemt, omdat de zekerheid van de schatting toeneemt.
Stel je voor dat je herhaaldelijk een steekproef neemt uit de populatie en hiervan telkens de t-waarde berekent. Hoe groter je steekproefgrootte, hoe minder de teststatistiek tussen de steekproeven zal verschillen.
Je neemt een aselecte steekproef van 10 Amerikaanse volwassenen en meet hun dagelijkse calciuminname.
De eenzijdige t-toets bepaalt wanneer een populatiegemiddelde afwijkt van een specifieke waarde. Je kent het populatiegemiddelde echter niet, dus moet je deze eerst schatten met behulp van het steekproefgemiddelde.
Je berekent dat het steekproefgemiddelde 820 mg is.
Door aan te nemen dat het populatiegemiddelde een bepaalde waarde heeft, leg je een beperking op aan de steekproef. De waarden in de steekproef moeten een gemiddelde hebben van 820 mg. Hierdoor is de laatste waarde niet vrij om te variëren, maar heeft deze slechts één mogelijke waarde.
Bijvoorbeeld: stel dat negen van de tien mensen in de steekproef een dagelijkse calciuminname hebben van 410, 1230, 870, 1110, 570, 390, 1030, 1080 en 639 mg. Dit betekent dat de tiende persoon een inname hebben van 880 mg moet hebben om op een steekproefgemiddelde van 820 mg uit te komen.
Door de beperking zijn slechts negen van de tien waarden vrij om te variëren. De teststatistiek, t, heeft 9 vrijheidsgraden.
Om de kritieke waarde te vinden, moet je dus de t-verdeling voor 9 vrijheidsgraden gebruiken. Als de t-waarde van de steekproef groter is dan kritieke waarde, verwerp je de nulhypothese.
Om een chi-kwadraattoets uit te voeren, vergelijk je de chi-kwadraat van een steekproef met een kritieke waarde. Om de juiste kritieke waarde te vinden, moet je de chi-kwadraatverdeling gebruiken met de juiste vrijheidsgraden.
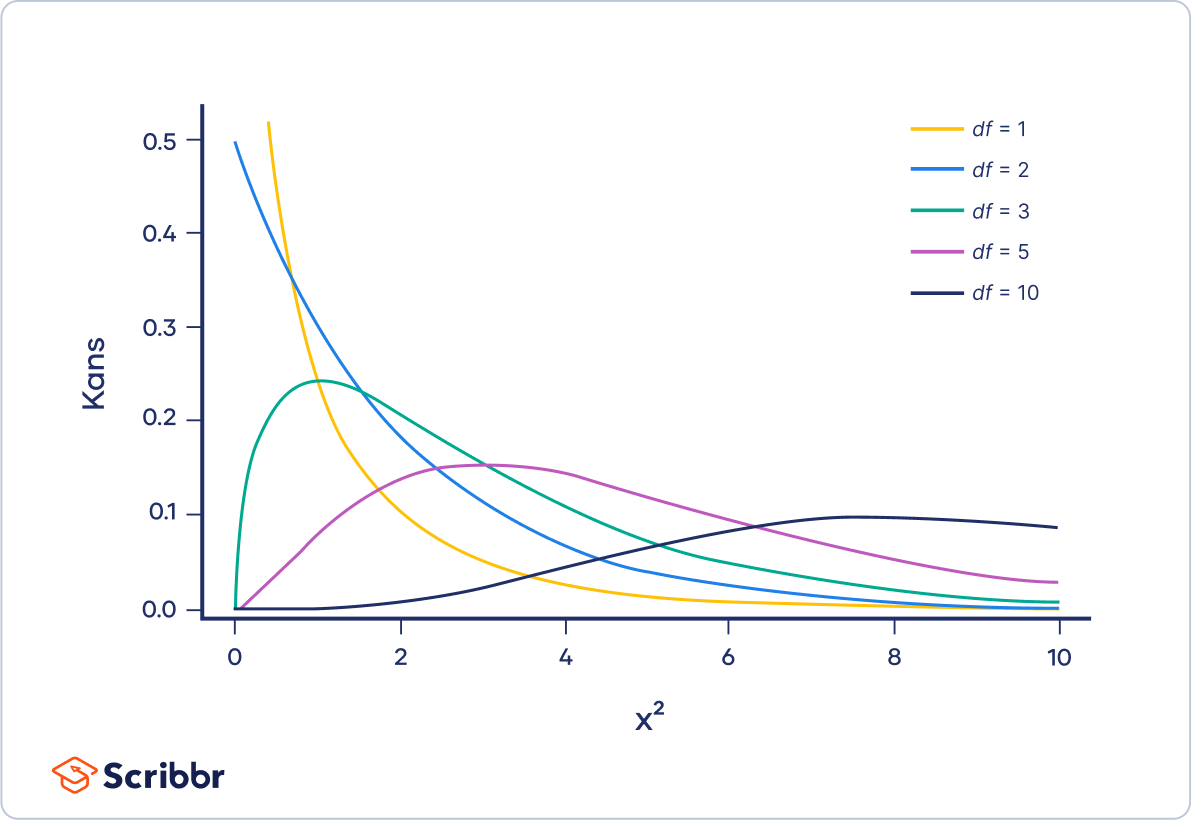
De nulverdeling van chi-kwadraat verandert met het aantal vrijheidsgraden, maar op een andere manier dan de t-verdeling:
- Als df < 3, dan heeft de kansverdeling de vorm van een omgedraaide “J”.
- Als df ≥ 3, dan is de kansverdeling bultvormig (hump-shaped), met de piek van de bult op X2 = df – 2. De bult is rechtsscheef (right-skewed), wat betekent dat de verdeling langer is aan de rechterkant van de piek.
- Als df > 90, dan is de chi-kwadraatverdeling bij benadering een normale verdeling.
Hoe bereken je de vrijheidsgraden?
De vrijheidsgraden van een statistiek zijn de steekproefgrootte min het aantal beperkingen. Meestal zijn de beperkingen de parameters die worden geschat als tussenstap bij de berekening van de statistiek.
n – r
Waarbij:
- n = de steekproefgrootte
- r = het aantal beperkingen (dat gewoonlijk hetzelfde is als het aantal geschatte parameters)
De vrijheidsgraden kunnen niet negatief zijn. Daarom kan het aantal geschatte parameters niet groter zijn dan de steekproefgrootte.
Specifieke formules voor toetsen
Het kan lastig zijn om het aantal vrijheidsgraden te bepalen. Daarom is het vaak gemakkelijker om formules te gebruiken die specifiek zijn voor bepaalde toetsen om zo de vrijheidsgraden van een toetsstatistiek te bepalen.
De onderstaande tabel geeft formules om de vrijheidsgraden van verschillende veelgebruikte toetsen te berekenen.
| Soort toets | Formule | Opmerking |
|---|---|---|
| Eenzijdige t-toets | df = n − 1 | |
| Onafhankelijke (ongepaarde) t-toets | df = n1 + n2 − 2 | Waarbij:
|
| Afhankelijke (gepaarde) t-toets | df = n − 1 | Waarbij:
|
| Enkelvoudige lineaire regressie | df = n − 2 | |
| Chi-kwadraattoets voor verdelingen (chi-square goodness of fit test) | df = k − 1 | Waarbij:
|
| Chi-kwadraattoets voor samenhang (chi-square test of independence) | df = (r − 1) * (c − 1) | Waarbij:
|
| One-way-ANOVA | Between-group df = k − 1 Within-group df = N − k Total df = N − 1 |
Waarbij:
|
Oefenvragen
Lees waarom zo veel studenten Scribbr inschakelen
Veelgestelde vragen over vrijheidsgraden (degrees of freedom)
- Wat gebeurt er met de vorm van de Student’s t-verdeling als de vrijheidsgraden toenemen?
-
Als de vrijheidsgraden toenemen, wordt de (student’s) t-verdeling minder leptokurtisch, wat betekent dat de kans op extreme waarden afneemt.
- Wat gebeurt er met de vorm van de chi-kwadraatverdeling als de vrijheidsgraden toenemen?
-
Als er slechts één of twee vrijheidsgraden zijn, heeft de chi-kwadraatverdeling de vorm van een omgekeerde “J”.
Als er drie of meer vrijheidsgraden zijn, heeft de verdeling de vorm van een rechtsscheve bult (hump).
Naarmate het aantal vrijheidsgraden verder toeneemt, wordt de bult minder rechtsscheef en verschuift de piek van de bult naar rechts. De verdeling gaat steeds meer lijken op een normale verdeling.
- Hoe toets ik een hypothese met behulp van de kritieke waarde van t?
-
Om een hypothese te toetsen met behulp van de kritieke waarde van t, volg je deze vier stappen:
- Bereken de t-waarde en vrijheidsgraden van je steekproef.
- Zoek de kritieke waarde van deze t-waarde in de t-tabel die hoort bij de juiste vrijheidsgraden.
- Bepaalde of de (absolute) t-waarde groter is dan de kritieke waarde van t.
- Verwerp de nulhypothese als de t-waarde van de steekproef groter is dan de kritieke waarde van t. Zo niet, dan verwerp je de nulhypothese niet.
Citeer dit Scribbr-artikel
Als je naar deze bron wilt verwijzen, kun je de bronvermelding kopiëren of op “Citeer dit Scribbr-artikel” klikken om de bronvermelding automatisch toe te voegen aan onze gratis Bronnengenerator.
Scharwächter, V. (2022, 15 augustus). Vrijheidsgraden (Degrees of Freedom) | Definitie & Formules. Scribbr. Geraadpleegd op 11 november 2024, van https://www.scribbr.nl/statistiek/vrijheidsgraden-degrees-of-freedom/
