Outliers (Uitbijters) Detecteren | Voorbeelden & Uitleg

Outliers (uitschieters of uitbijters) zijn extreme waarden die verschillen van de meeste andere observatiepunten in een dataset. Ze kunnen een grote impact hebben op je statistische analyses en de resultaten van je hypothesetoetsing scheeftrekken (skew).

Het is belangrijk om potentiële uitschieters in je dataset zorgvuldig te identificeren en ze op de juiste manier te behandelen voor accurate resultaten.

Wat zijn outliers?

Outliers (uitschieters of uitbijters) zijn de waarden aan de uiterste uiteinden van een dataset.

Sommige uitschieters vertegenwoordigen echte waarden door natuurlijke variatie in de populatie. Andere uitschieters kunnen het gevolg zijn van onjuiste invoer van data, storingen in de apparatuur of andere meetfouten.

Een outlier is niet altijd “dirty” of onjuiste data, dus het is belangrijk om voorzichtig te zijn bij het opschonen van je data (data cleaning). Wat je met een outlier zou moeten doen, hangt af van de vermoede oorzaak van de outlier.

Echte uitschieters (true outliers)

Echte uitschieters moet je altijd in je dataset houden, omdat deze punten natuurlijke variaties in je steekproef vertegenwoordigen.

Echte uitschieters komen ook voor bij variabelen met een scheve verdeling, waarbij veel data ver van het gemiddelde in één richting liggen (i.e., de verdeling is langer aan de rechter- of linkerkant van de piek). Het is belangrijk de juiste statistische toets of meting te kiezen als je er sprake is van skewness of als je veel uitschieters hebt.

Overige uitschieters

Uitschieters die niet de echte waarden vertegenwoordigen, kunnen afkomstig zijn van veel verschillende bronnen:

• Meetfouten
• Fouten bij het invoeren of verwerken van data
• Niet-representatieve steekproef

Dit soort uitschieters is problematisch omdat de meetpunten onnauwkeurig zijn en je onderzoeksresultaten kunnen vertekenen.

In de praktijk kan het moeilijk zijn om verschillende soorten uitschieters uit elkaar te houden. Je kunt berekeningen en statistische methoden gebruiken om uitschieters op te sporen, maar ze classificeren als echte of onjuiste uitschieters is meestal een subjectief proces.

Hoeveel fouten bevat jouw scriptie?

De taalexperts van Scribbr verbeteren gemiddeld 150 fouten per 1000 woorden. Benieuwd wat er precies wordt verbeterd? Verschuif de cursor van links naar rechts!

Scriptie nakijken op taal

Vier manieren om outliers te berekenen

Je kunt uit verschillende manieren kiezen om outliers op te sporen, afhankelijk van je tijd en middelen.

Sorteermethode

Je kunt kwantitatieve variabelen sorteren van laag naar hoog en zo scannen op extreem lage of extreem hoge waarden. Markeer alle extreme waarden die je vindt.

Dit is een simpele manier om snel na te gaan of je bepaalde datapunten moet onderzoeken voordat je statistische analyses uitvoert.

Visualisaties

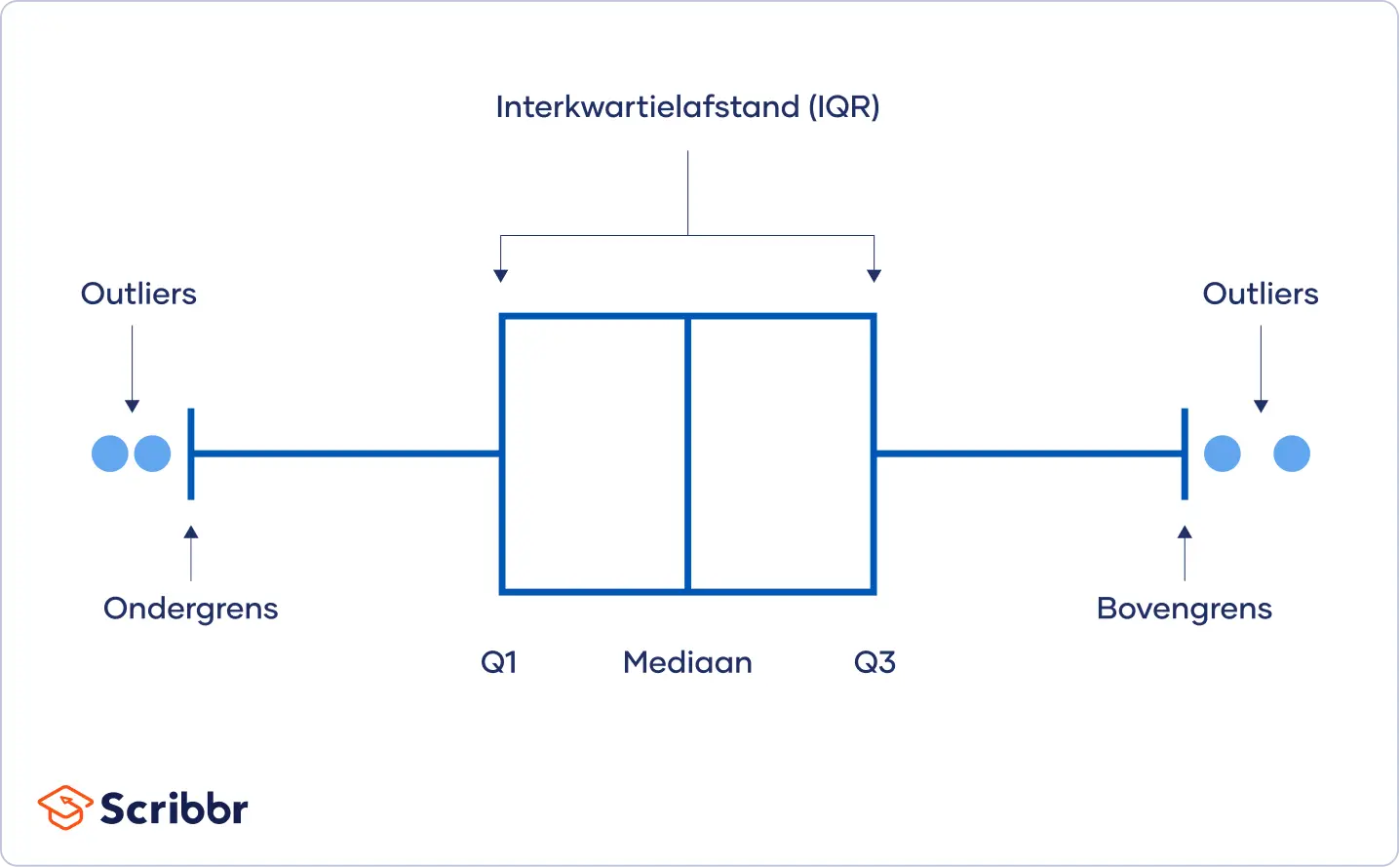
Je kunt software gebruiken om je data te visualiseren met een boxplot, of een box-and-whisker plot, zodat je in één oogopslag de verdeling van de data kunt zien. In dit soort diagrammen worden de minimum- en maximumwaarden (het bereik), de mediaan en de interkwartielafstand van je data aangegeven.

Veel computerprogramma’s markeren een uitschieter in een grafiek met een sterretje (*, asterisk). Deze liggen dan buiten de grenzen van de grafiek.

Statistische detectie

Statistische detectie van uitschieters houdt in dat statistische toetsen of procedures worden toegepast om extreme waarden te identificeren.

Je kunt extreme waarden omzetten in z-scores die je vertellen hoeveel standaardafwijkingen ze van het gemiddelde verwijderd zijn.

Als een waarde een z-score heeft die laag of hoog genoeg is, kan deze als een uitschieter worden beschouwd. Als vuistregel geldt dat waarden met een z-score groter dan 3 of kleiner dan -3 vaak als uitschieter worden aangemerkt.

Interkwartielafstand

De interkwartielafstand (interquartile range, IQR) geeft het bereik aan van de middelste helft van je dataset. Je kunt de IQR gebruiken om “hekken” (grenzen) rondom je data te maken en vervolgens de uitschieters te definiëren als alle waarden die buiten de hekken vallen.

Deze methode is nuttig als je enkele waarden hebt aan de uiterste uiteinden van je verdeling, maar niet zeker weet of één van deze als uitschieter kan worden beschouwd.

Methode voor interkwartielafstand

1. Sorteer je data van laag naar hoog
2. Bepaal het eerste kwartiel (Q1), de mediaan, en het derde kwartiel (Q3)
3. Bereken je IQR = Q3 – Q1
4. Bereken je bovengrens = Q3 + (1.5 * IQR)
5. Bereken je ondergrens = Q1 – (1.5 * IQR)
6. Gebruik je gevonden grenzen om eventuele uitschieters te markeren

Je uitschieters zijn alle waarden die groter zijn dan je bovengrens of kleiner dan je ondergrens.

Voorbeeld: De interkwartielafstand gebruiken om uitschieters te vinden

Hieronder vind je een stappenplan met voorbeeld om de populaire IQR-methode toe te passen om uitschieters te identificeren.

Je dataset heeft 11 waarden. Je hebt een paar extreme waarden in je dataset, dus gebruik je de IQR-methode om te controleren of dit uitschieters zijn.

Stap 1: Sorteer je data van laag naar hoog

Eerst sorteer je de data in oplopende volgorde.

Stap 2: Identificeer de mediaan, het eerste kwartiel (Q1) en het derde kwartiel (Q3)

De mediaan is de waarde precies in het midden van je dataset als je alle waarden hebt gerangschikt van laag naar hoog.

Aangezien je 11 waarden hebt, is je mediaan de 6de waarde. De mediaanwaarde is 31.

Vervolgens gebruik je de exclusieve methode om Q1 en Q3 te identificeren. Dit betekent dat je de mediaan uit je berekeningen verwijdert.

Het eerste kwartiel (Q1) is de waarde in het midden van de eerste helft van je dataset, exclusief de mediaan. De waarde van het eerste kwartiel is 26.

Het derde kwartiel (Q3) ligt in het midden van de tweede helft van je dataset, exclusief de mediaan. De waarde van het derde kwartiel is 41.

Stap 3: Bereken je IQR

De IQR is het bereik van de middelste helft van je dataset. Trek Q1 af van Q3 om om de IQR te berekenen.

Stap 4: Bereken je bovengrens

De bovenste grens is de grens van het derde kwartiel. Alle waarden die de bovenste grens overschrijden, zijn uitschieters.

Stap 5: Bereken je ondergrens

De onderste grens is de grens van het eerste kwartiel. Alle waarden onder de onderste grens zijn uitschieters.

Stap 6: Gebruik je grenzen om uitschieters te vinden

Ga terug naar je gesorteerde dataset van stap 1 en markeer alle waarden die groter zijn dan de bovengrens en kleiner dan de ondergrens. Dit zijn je outliers.

• Bovengrens = 63.5
• Ondergrens = 3.5

Je vindt één uitschieter, 64, in je dataset.

Omgaan met outliers

Zodra je je uitschieters hebt geïdentificeerd, beslis je wat je ermee doet. Je kunt ervoor kiezen om ze te behouden of te verwijderen uit je dataset. Dit is vergelijkbaar met de keuze die je moet maken als je te maken krijgt met ontbrekende data (missing data of missing values).

Overweeg voor elke uitschieter of het een echte waarde is of een fout:

• Komt de outlier overeen met andere metingen van dezelfde deelnemer?
• Is de meting volkomen onmogelijk of kan deze redelijkerwijs uit de populatie afkomstig zijn?
• Wat is de meest waarschijnlijke bron van de uitschieter? Is het een natuurlijke variatie of een fout?

Over het algemeen moet je uitschieters zoveel mogelijk accepteren, tenzij het duidelijk is dat ze fouten of onjuiste data vertegenwoordigen.

Outliers behouden

Net als bij ontbrekende waarden is de meeste voorzichtige en conservatieve optie het behouden van outliers in je dataset. Uitschieters behouden is meestal de beste optie als je niet zeker weet of het fouten zijn.

Met een grote steekproef zijn uitschieters gebruikelijk en is de kans groter dat uitschieters zich voordoen. Als je steekproef groot genoeg is, zullen je uitschieters minder invloed hebben op je resultaten. De centrale tendens en de spreiding van je data worden niet zo sterk beïnvloed door een aantal extreme waarden als je een groot aantal waarden hebt.

Als je een kleine dataset hebt, kan het ook slim zijn om uitschieters te behouden. Je wilt namelijk niet te weinig data overhouden, omdat anders de statistische power van je onderzoek afneemt. Als je dataset veel uitschieters bevat, kun je een statistische toets gebruiken die beter tegen uitschieters bestand is. Niet-parametrische toetsen lenen zich hier beter voor.

Outliers verwijderen

Outliers verwijderen betekent dat je extreme waarden uit je dataset verwijdert voordat je analyses uitvoert. Het doel is om alle onjuiste data te verwijderen, maar de echte extreme waarden wel te behouden.

Dit is meestal een lastige procedure, omdat het vaak onmogelijk is om de twee soorten uitschieters van elkaar te onderscheiden. Het verwijderen van echte uitschieters kan leiden tot een vertekende dataset en een verkeerde conclusie.

Daarom mogen uitschieters alleen worden verwijderd als daar gegronde redenen voor zijn. Het is belangrijk om elke uitschieter die je verwijdert én de reden voor het verwijderen te documenteren, zodat andere onderzoekers je proces kunnen volgen.

Veelgestelde vragen over outliers

Waarom zijn outliers belangrijk?

Outliers (uitschieters) kunnen een grote impact hebben op je statistische analyses. Ook kunnen ze de resultaten van een hypothesetoetsing vertekenen als ze onjuist zijn.

Deze extreme waarden kunnen ook de statistische power van je toets beïnvloeden, waardoor het moeilijk wordt een echt effect op te sporen, als er wel een effect is (Type II-fout).

How vind ik outliers in mijn data?

Je kunt kiezen uit vier manieren om outliers te detecteren:

1. Het sorteren van je waarden van laag naar hoog en het controleren van minimum- en maximumwaarden.
2. Het visualiseren van je data met een boxplot en zoeken naar uitschieters.
3. De interkwartielafstand gebruiken om de grenzen voor je data te vinden.
4. Statistische toetsen uitvoeren om extreme waarden te identificeren.

Wanneer moet ik een outlier verwijderen uit mijn dataset?

Je kunt outliers het beste alleen verwijderen als je daar een goede reden voor hebt.

Sommige uitschieters vertegenwoordigen natuurlijke variatie in de populatie en deze mogen niet worden verwijderd uit je dataset. Dit zijn echte uitschieters.

Andere uitschieters zijn problematisch en moeten worden verwijderd uit je dataset. Deze uitschieters zijn meetfouten, invoer- of verwerkingsfouten, of data uit een niet-representatieve steekproef.