Two-Way ANOVA | Interpretatie, Uitvoering & Voorbeelden

Een two-way ANOVA schat hoe het gemiddelde van een kwantitatieve variabele verandert voor verschillende niveaus van twee categorische variabelen.

ANOVA (analysis of variance) is een statistische toets die wordt gebruikt om het verschil tussen de gemiddelden van meer dan twee groepen te analyseren.

Wanneer gebruik je een two-way ANOVA?

Je kunt een two-way ANOVA gebruiken als je data hebt verzameld voor één kwantitatieve afhankelijke variabele en twee categorische onafhankelijke variabelen. De onafhankelijke variabelen moeten uit meerdere niveaus (e.g., groepen, typen) bestaan.

• Een kwantitatieve variabele vertegenwoordigt de hoeveelheden of tellingen van dingen. Deze variabele kan worden verdeeld om een groepsgemiddelde te vinden.

• Een categorische variabele vertegenwoordigt soorten of categorieën van dingen. Een niveau is een individuele categorie binnen de categorische variabele.

Je moet voldoende observaties in je dataset hebben om het gemiddelde van de kwantitatieve afhankelijke variabele te kunnen vinden bij elke combinatie van niveaus van de onafhankelijke variabelen.

Hoe werkt een two-way ANOVA?

Een ANOVA test op significantie met behulp van de F-test voor statistische significantie. De F-test is een groepsgewijze vergelijkingstoets, wat betekent dat de variantie in het gemiddelde van elke groep wordt vergeleken met de totale variantie in de afhankelijke variabele.

Als de variantie binnen groepen kleiner is dan de variantie tussen groepen, zal de F-test een hogere F-waarde opleveren. Er is dan een grotere waarschijnlijkheid dat het waargenomen verschil echt is en niet het gevolg van toeval.

Een two-way ANOVA met interactie test drie nulhypothesen tegelijkertijd:

• Er is geen verschil in groepsgemiddelden van de eerste onafhankelijke variabele, ongeacht het niveau.
• Er is geen verschil in groepsgemiddelden van de tweede onafhankelijke variabele, ongeacht het niveau.
• Het effect van de ene onafhankelijke variabele hangt niet af van het effect van de andere onafhankelijke variabele (ook wel: geen interactie-effect).

Een two-way ANOVA zonder interactie (ook wel een additieve two-way ANOVA genoemd) test alleen de eerste twee hypothesen.

Aannames van two-way ANOVA

Om een two-way ANOVA te kunnen gebruiken, moeten je data aan bepaalde aannames voldoen. Deze komen grotendeels overeen met de algemene assumpties voor iedere parametrische toets:

1. Kwantitatieve, continue afhankelijke variabele: je afhankelijke variabele moet naast kwantitatief ook continu van aard zijn, wat betekent dat het interval- of ratiometingen zijn. Dit betekent dat de afhankelijke variabele binnen het interval- of rationiveau iedere waarde kan aannemen.
2. Twee of meer categorische, onafhankelijke groepen: de onafhankelijke variabelen moeten ieder uit twee of meer categorische, onafhankelijke groepen (niveaus) bestaan.
3. Homogeniteit van variantie (ook wel homoscedasticiteit genoemd): de variatie rond het gemiddelde voor elke groep die vergeleken wordt, moet voor alle groepen gelijk zijn. Als je data niet aan deze aanname voldoen, kun je mogelijk een niet-parametrische toets gebruiken, zoals de Kruskal-Wallis toets.
4. Onafhankelijkheid van observaties: je onafhankelijke variabelen mogen niet van elkaar afhankelijk zijn (i.e., de ene mag de andere niet veroorzaken). Dit is onmogelijk te toetsen met categorische variabelen. Daardoor kan deze assumptie alleen gewaarborgd worden door een goed experimenteel design. Daarnaast moeten je observaties unieke waarnemingen zijn (i.e., je waarnemingen mogen niet gegroepeerd zijn binnen locaties of individuen). Als je data niet aan deze aanname voldoen, kun je een ANOVA met blokkerende variabele en/of een ANOVA met herhaalde metingen (within-subjects) gebruiken.
5. Geen significante outliers: de aanwezigheid van outliers kan de validiteit van de resultaten van je two-way ANOVA beïnvloeden.
6. Normaalverdeelde afhankelijke variabele: de waarden van de afhankelijke variabele moeten een normale verdeling (bell curve) volgen. Als je data niet aan deze aanname voldoen, kun je een datatransformatie proberen (i.e., dezelfde functie toepassen op alle waarden van de variabele).

Two-way ANOVA uitvoeren

De voorbeelddataset voor het experiment over gewasopbrengst bevat waarnemingen over:

• Uiteindelijke gewasopbrengst (in bushels per acre)
• Soort kunstmest (type 1, 2 of 3)
• Plantdichtheid (1 = lage dichtheid, 2 = hoge dichtheid)
• Locatie van plant in het veld (blok 1, 2, 3 of 4)

Klik op de blauwe button hieronder om de dataset zelf te downloaden.

Voorbeeld dataset voor two-way ANOVA

De two-way ANOVA zal testen of de onafhankelijke variabelen (i.e., kunstmestsoort en plantdichtheid) een effect hebben op de afhankelijke variabele (i.e., uiteindelijke gewasopbrengst). Maar er zijn nog andere mogelijke bronnen van variatie in de data waar we rekening mee willen houden:

• Het experimentele design is in blokken opgezet, dus we willen weten of het blok een verschil maakt voor de gemiddelde gewasopbrengst.
• Ook willen we nagaan of er een interactie-effect is tussen de onafhankelijke variabelen. Het is bijvoorbeeld mogelijk dat de plantdichtheid van invloed is op het vermogen van de planten om kunstmest op te nemen.

Omdat er meerdere potentiële relaties tussen de variabelen zijn, kunnen we drie modellen vergelijken:

1. Een two-way ANOVA zonder interactie of blokkerende variabele (ook wel een additieve two-way ANOVA genoemd).
2. Een two-way ANOVA met interactie, maar zonder blokkerende variabele.
3. Een two-way ANOVA met interactie en met blokkerende variabele.

Model 1 gaat ervan uit dat er geen interactie is tussen de onafhankelijke variabelen. Model 2 neemt aan dat er wel een interactie is tussen de onafhankelijke variabelen. En model 3 gaat ervan uit dat er een interactie is tussen de onafhankelijke variabelen, en dat de blokkerende variabele een belangrijke bron van variatie in de data is.

Door alle drie de modellen in een two-way ANOVA uit te voeren en vervolgens te vergelijken, kan worden nagegaan welke variabelen, en in welke combinaties, belangrijk zijn voor de beschrijving van de data, en of het blok van belang is voor de gemiddelde gewasopbrengst.

Two-way ANOVA uitvoeren in R

Hieronder laten we je zien hoe je de analyses voor deze two-way ANOVA uitvoert in het statistische programma R.

Je kunt de uitvoering van deze two-way ANOVA in R zelf proberen door onderstaande voorbeelddataset te downloaden.

Voorbeeld-dataset voor two-way ANOVA

Na het laden van de data in de R-omgeving, zullen we elk van de drie modellen creëren met het commando aov(), en ze vervolgens vergelijken met het commando aictab().

Het eerste model voorspelt geen interactie tussen de onafhankelijke variabelen, dus voegen we ze samen met een “+”.

In het tweede model wordt het interactie-effect wel gemeten. Om na te gaan of de interactie tussen de soort kunstmest en plantdichtheid de uiteindelijke gewasopbrengst beïnvloedt, gebruik je een “*” om aan te geven dat je ook het interactie-effect wilt meten.

Omdat de gewasopbrengsten binnen blokken werden gerandomiseerd, wordt deze variabele als een blokkerende variabele toegevoegd aan het derde model. Hierdoor kun je de two-way ANOVA’s met en zonder de blokkerende variabele vergelijken om te kijken of het blok van belang is.

Vergelijking modellen

Nu kunnen we uitzoeken welk model het beste past bij de data met behulp van de AIC (Akaike Information Criterion) modelselectie.

AIC berekent het best passende model door het model te vinden dat de grootste hoeveelheid variatie in de responsvariabele verklaart met de minste parameters. In R kun je een modelvergelijking uitvoeren met de functie aictab().

library(AICcmodavg)

model.set <- list(two.way, interaction, blocking)
model.names <- c("two.way", "interaction", "blocking")

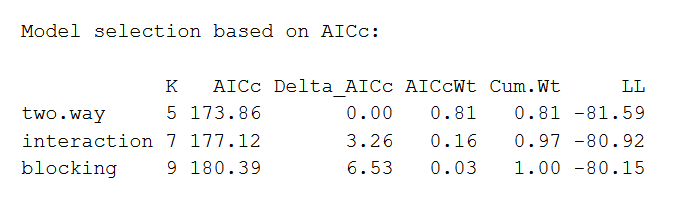
aictab(model.set, modnames = model.names)

De output van de AIC ziet er als volgt uit:

Het AIC-model dat het beste past wordt als eerste vermeld, gevolgd door het op één na beste model, enzovoorts. Uit deze vergelijking blijkt dat de two-way ANOVA zonder interactie of blokkerende variabelen het beste past bij de data.

Resultaten interpreteren

Je kunt de samenvatting van de two-way ANOVA in R bekijken met de functie summary(). Hier worden de resultaten van het eerste model bekeken, die het beste passen bij de data.

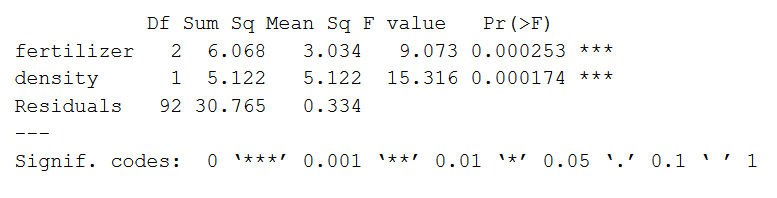
De output van de samenvatting ziet er als volgt uit:

De samenvatting van het model weergeeft eerst de geteste onafhankelijke variabelen (“fertilizer” en “density”). Daarna volgt de restvariantie (“Residuals”). De restvariantie is de variatie in de afhankelijke variabele die niet door de onafhankelijke variabelen wordt verklaard.

De volgende kolommen geven alle informatie die nodig is om het model te interpreteren:

• De kolom Df toont de vrijheidsgraden voor elke variabele (i.e., het aantal niveaus in de variabele min 1).
• De kolom Sum Sq is de som van de kwadraten (sum of squares, ook wel de totale variatie). Dit is de variatie tussen de groepsgemiddelden en het totale gemiddelde dat door die variabele wordt verklaard.
• De kolom Mean Sq toont de gemiddelde som van de kwadraten (i.e., de som van de kwadraten gedeeld door de vrijheidsgraden).
• De kolom F-value is de teststatistiek van de F-test (i.e., het gemiddelde kwadraat van de variabele gedeeld door het gemiddelde kwadraat van elke parameter).
• De kolom Pr(>F) is de p-waarde van de F-statistiek. Deze waarde geeft aan hoe waarschijnlijk het is dat de F-waarde berekend uit de F-test zou zijn opgetreden als de nulhypothese van geen verschil waar was.

Uit deze analyse blijkt dat zowel het soort kunstmest als de plantdichtheid een significant deel van de variatie in de gemiddelde gewasopbrengst verklaren (p-waarden < 0.001).

Post-hoc test

ANOVA vertelt je welke parameters significant zijn, maar niet welke niveaus daadwerkelijk van elkaar verschillen. Om dit te testen kun je een post-hoc test gebruiken. Tukey’s Honestly-Significant-Difference (TukeyHSD) test laat zien welke groepen van elkaar verschillen.

De output van de Tukey test ziet er als volgt uit:

Deze output toont de paarsgewijze verschillen tussen de drie soorten kunstmest (“$fertilizer”) en tussen de twee niveaus van plantdichtheid (“$density”), met het gemiddelde verschil (“diff”), de onder- en bovengrens van het 95%-betrouwbaarheidsinterval (“lwr” en “upr”) en de p-waarde van het verschil (“p-adj”).

Uit de resultaten van de post-hoc blijkt dat er significante verschillen (p > 0.05) zijn tussen:

• Kunstmest 3 en 1;
• Kunstmest 3 en 2;
• De twee niveaus van plantdichtheid.

Er is geen significant verschil tussen kunstmest 1 en 2.

Resultaten rapporteren

Je kunt de resultaten van je two-way ANOVA rapporteren in je onderzoeksresultaten aan de hand van de output van je model.

Bij de rapportage van je resultaten moet je de F-statistiek, de vrijheidsgraden en de p-waarde van je output vermelden.

In de discussie van je paper of scriptie kun je deze bevindingen bespreken.

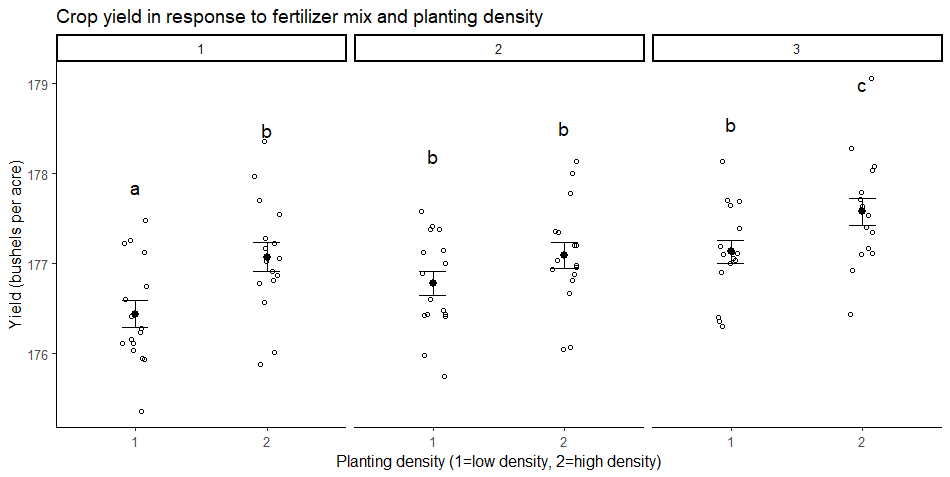
Je kunt ook een grafiek maken van je bevindingen om je resultaten te illustreren.

Je grafiek moet de groepsgewijze vergelijkingen bevatten die in de ANOVA zijn getest, met de ruwe data, samenvattende statistieken (hier getoond als gemiddelden en standaard error-staven), en letters of significantiewaarden boven de groepen om aan te geven welke groepen significant verschillen van anderen.

Veelgestelde vragen over two-way ANOVA

Hoe wordt statistische significantie berekend in een ANOVA?

Bij een ANOVA is de nulhypothese dat er geen verschil is tussen de groepsgemiddelden. Als een groep significant verschilt van het algemene groepsgemiddelde, dan zal de ANOVA een statistisch significant resultaat rapporteren.

Significante verschillen tussen groepsgemiddelden worden berekend met behulp van een F-statistiek, die de verhouding weergeeft tussen de gemiddelde som van de kwadraten (de variantie die door de onafhankelijke variabele wordt verklaard) en de gemiddelde kwadratische fout (de variantie die overblijft).

Als de F-statistiek hoger is dan de kritieke waarde (de waarde van F die overeenkomt met je alfa-waarde, meestal 0.05), dan wordt het verschil tussen groepen statistisch significant geacht.

Wat is een ANOVA en waarvoor wordt de toets gebruikt?

ANOVA staat voor Analysis of Variance, oftewel variantieanalyse, en wordt gebruikt om gemiddelden van meer dan twee groepen met elkaar te vergelijken. Het is een uitbreiding van de t-toets, die het gemiddelde van maximaal twee groepen met elkaar vergelijkt.

Wat is een factoriële ANOVA?

Een factoriële ANOVA is elke ANOVA die meer dan één categorische onafhankelijke variabele gebruikt. Een two-way ANOVA is een soort factoriële ANOVA.

Enkele voorbeelden van scenario’s waarin je factoriële ANOVA’s gebruikt, zijn:

• Het toetsen van de gecombineerde effecten van vaccinatie (gevaccineerd of niet gevaccineerd) en gezondheidsstatus (gezond of al bestaande aandoening) op de mate van griepinfectie in een populatie.

• Het toetsen van de effecten van burgerlijke staat (gehuwd, ongehuwd, gescheiden, weduwnaar), beroepsstatus (zelfstandig, werkend, werkloos, gepensioneerd) en familiegeschiedenis (geen familiegeschiedenis, enige familiegeschiedenis) op de incidentie van depressie in een populatie.

• Het toetsen van effecten van het soort voeding (soort A, B of C) en stalbezetting (niet vol, enigszins vol, zeer vol) op het eindgewicht van kippen in een commercieel landbouwbedrijf.

Wat is een one-way ANOVA?

Je gebruikt een one-way-ANOVA wanneer één groepsvariabele (onafhankelijke variabele) de groepen bepaalt en er maar één afhankelijke variabele is.

Voorbeeld: Je vergelijkt de gemiddelde lengte van verschillende typen sporters, zoals voetballers, turners en volleyballers. Het type sport dat iemand beoefent, is in dit geval de enige groepsvariabele en lengte is de enige afhankelijke variabele.

Wat is het verschil tussen een kwantitatieve en categorische variabele?

Er kan een onderscheid worden gemaakt tussen kwantitatieve en categorische variabelen:

• Bij kwantitatieve variabelen representeren de data hoeveelheden (zoals een lengte, gewicht, leeftijd).
• Bij categorische variabelen representeren de data groepen, zoals een ranking (bijvoorbeeld de eindposities bij het songfestival), classificaties (bijvoorbeeld kledingmerken), en binaire verdelingen (zoals kop of munt).

Wat is een two-way ANOVA?

Je gebruikt een two-way-ANOVA (ook wel factorial ANOVA) als je twee of meer groepsvariabelen (onafhankelijke variabelen) in je conceptueel model hebt.

Voorbeeld: Je vergelijkt de gemiddelde lengte van verschillende typen sporters én hun gender. Er wordt dan niet alleen getest of het gemiddelde verschilt voor volleyballers en turners en voetballers, maar ook voor mannen, vrouwen en mensen met een ander gender, én of er eventuele interactie-effecten zijn.