De t-verdeling (t-distribution) begrijpen | Met voorbeelden
De t-verdeling (ook wel t-distribution of Student’s t-distribution genoemd) wordt gebruikt als de data bij benadering normaal verdeeld zijn (en dus een klokvorm volgen), maar waarbij de populatievariantie onbekend is. De variantie in een t-verdeling wordt geschat op basis van het aantal vrijheidsgraden van de dataset (totaal aantal waarnemingen min 1).
De t-verdeling is een variant op de normale verdeling, maar deze wordt gebruikt voor kleinere steekproeven, waarbij de variantie onbekend is.
Bij statistiek wordt de t-verdeling meestal gebruikt om:
- De kritische waarden voor een betrouwbaarheidsinterval te vinden als de data ongeveer normaal verdeeld zijn.
- De corresponderende p-waarde te vinden van een statistische toets die de t-verdeling gebruikt (t-toets, regressieanalyse).
Wat is een t-verdeling?
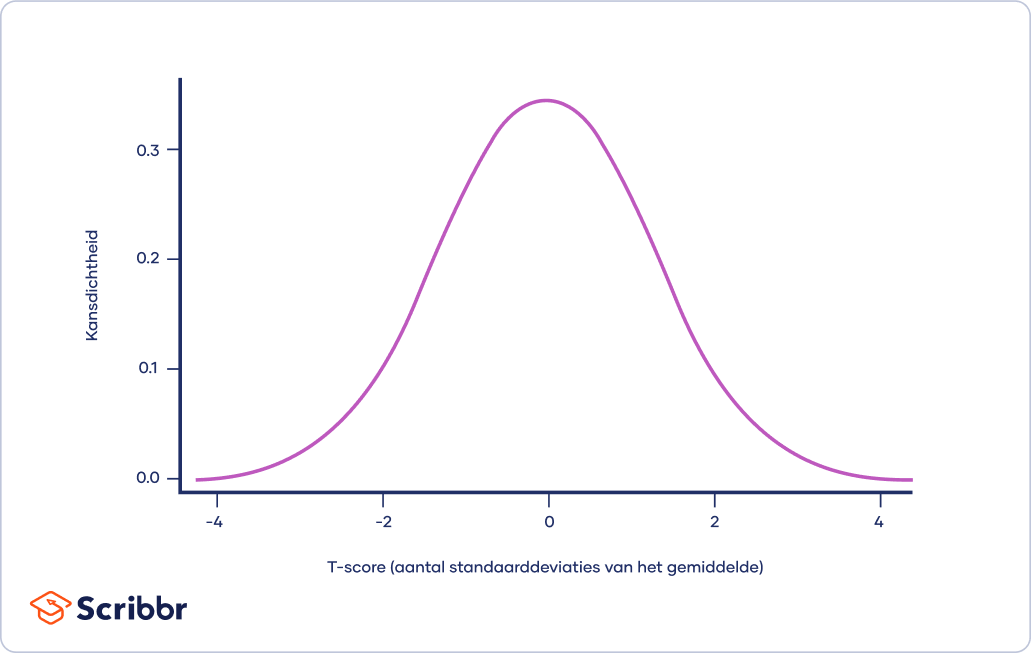
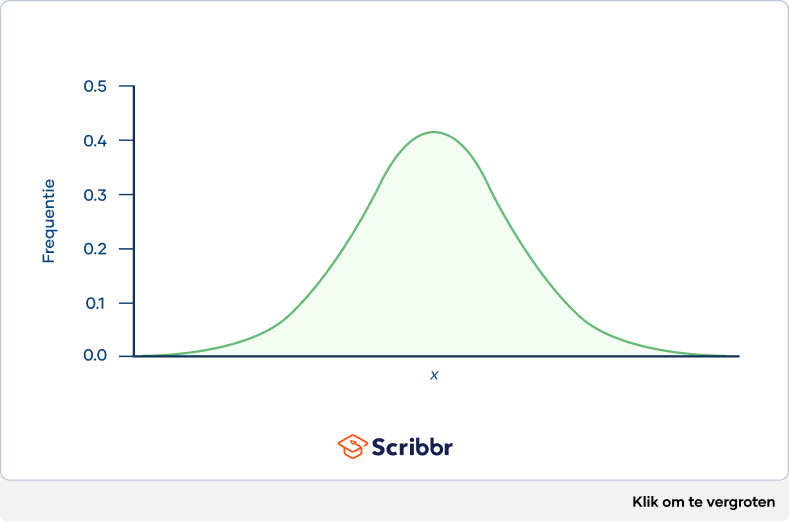
De t-verdeling is een variant op de normale verdeling die wordt gebruikt voor kleinere steekproeven. Normaal verdeelde gegevens vormen een klokvorm als je ze plot in een grafiek. Hierbij zijn er meer waarnemingen in de buurt van het gemiddelde dan in de staarten.
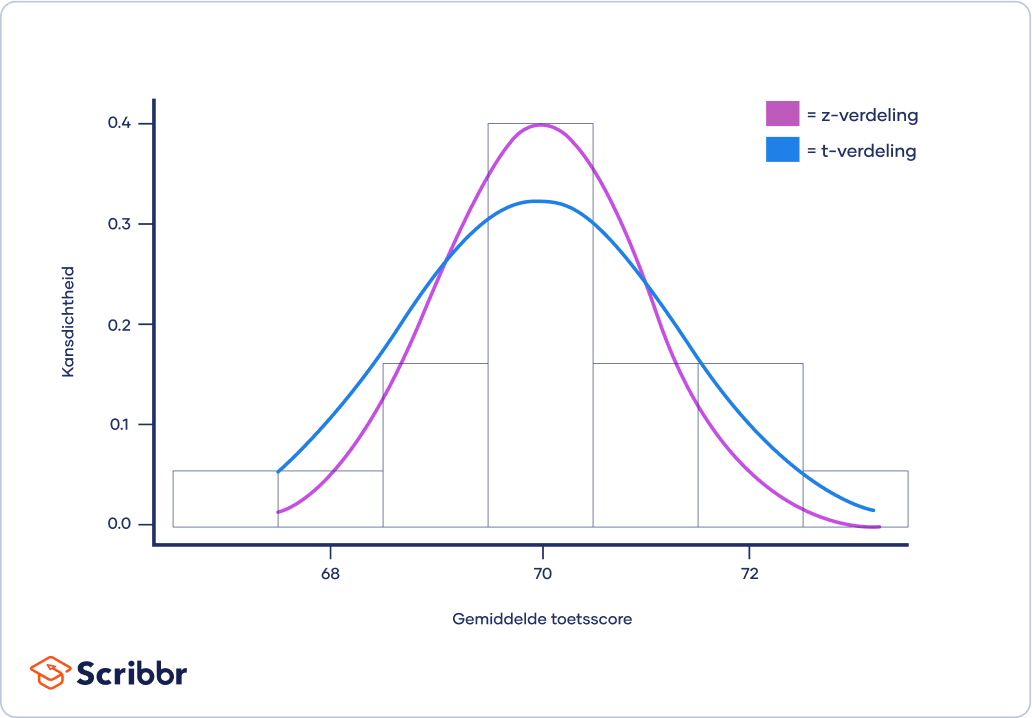
Het is een meer conservatieve vorm van de standaardnormale verdeling (ook wel z-verdeling of standard normal distribution genoemd). Dit betekent dat de t-verdeling een lagere kansdichtheid geeft voor het centrum en een hogere kansdichtheid voor de staarten dan de standaard normaleverdeling.
Lees waarom zo veel studenten Scribbr inschakelen
T-verdeling en de standaardnormale verdeling
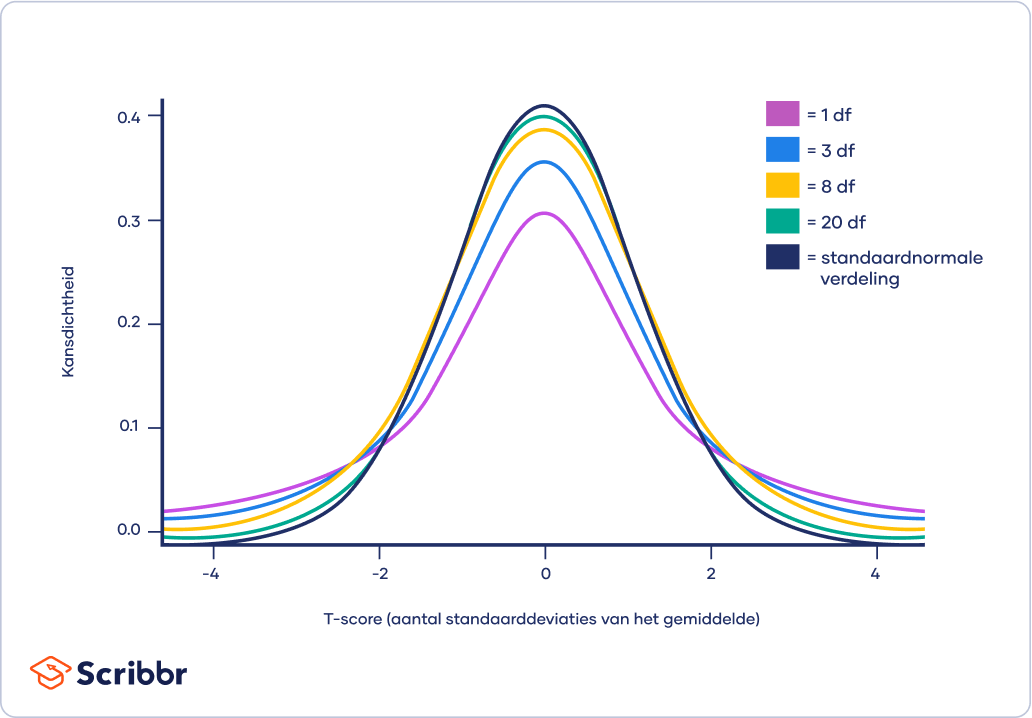
Naarmate het aantal vrijheidsgraden (totaal aantal waarnemingen min 1) toeneemt, zal de t-verdeling steeds dichter bij de standaardnormale verdeling (z-verdeling) komen te liggen, totdat ze nagenoeg hetzelfde zijn.
Boven 30 vrijheidsgraden komt de t-verdeling ongeveer overeen met de z-verdeling. Daarom gebruik je voor grote steekproeven de z-verdeling in plaats van de t-verdeling.
De z-verdeling wordt verkozen boven de t-verdeling, omdat de variantie bekend is bij de z-verdeling. Bij de t-verdeling wordt de variantie slechts geschat op basis van het aantal vrijheidsgraden. Hierdoor kunnen nauwkeurigere schattingen worden gemaakt met behulp van de z-verdeling.
T-verdeling en t-scores
Een t-score is het aantal standaarddeviaties van het gemiddelde in een t-verdeling. Je kunt een t-score opzoeken in een t-tabel of een online calculator voor de t-score gebruiken.
Bij statistiek worden t-scores voornamelijk gebruikt om de volgende waarden te bepalen:
- De boven- en ondergrenzen van een betrouwbaarheidsinterval als de data ongeveer normaal verdeeld zijn.
- De p-waarde van de teststatistiek voor t-toetsen en regressieanalyses.
T-scores en betrouwbaarheidsintervallen
Betrouwbaarheidsintervallen gebruiken t-scores om de boven- en ondergrenzen van het voorspellingsinterval te berekenen. De t-score die wordt gebruikt om de boven- en ondergrenzen te bepalen, wordt ook wel de kritische waarde van t of t* genoemd.
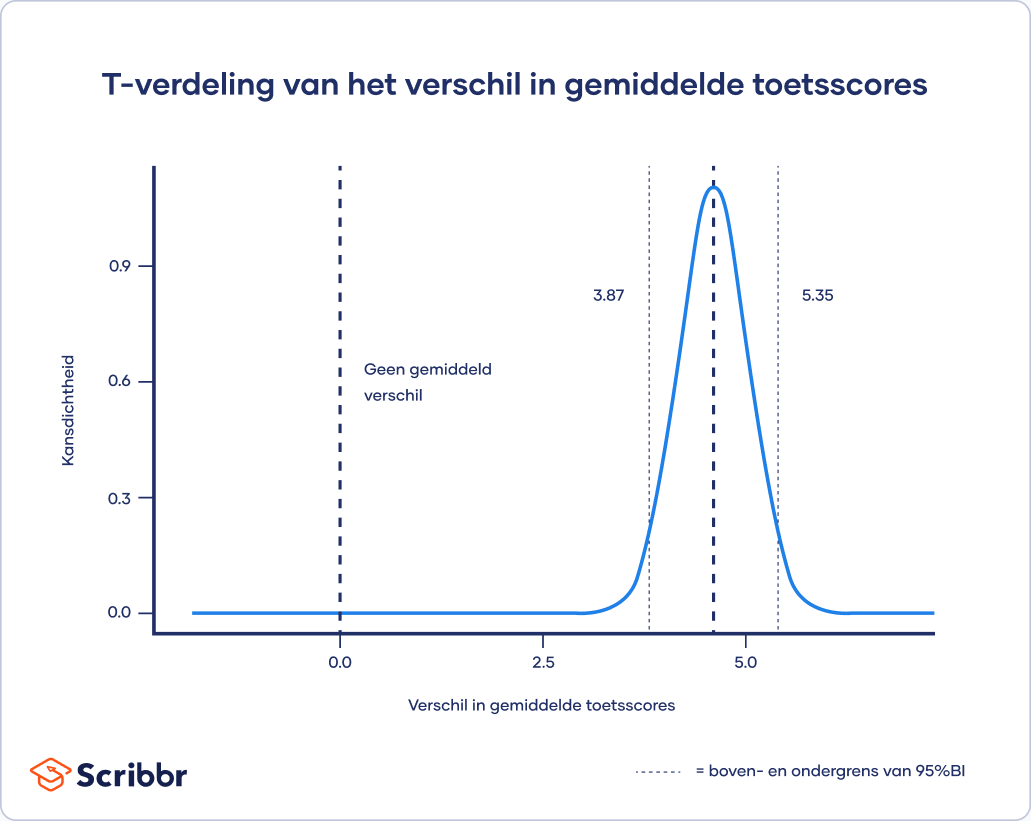
Met behulp van een tweezijdige t-toets schat je het verschil tussen de twee werkgroepen, evenals het betrouwbaarheidsinterval rond die schatting. Uit de t-toets blijkt dat het verschil in gemiddelde score tussen werkgroep 1 en werkgroep 2 gelijk is aan 4.61, met een 95% betrouwbaarheidsinterval van 3.87 tot 5.35.
Het betrouwbaarheidsinterval [3.87 – 5.35] bevat niet de waarde 0 (en ligt ver van 0 af), waardoor het onwaarschijnlijk is dat dit verschil in toetsscores wordt veroorzaakt door toeval of willekeurige factoren.
T-scores en p-waarden
Statistische toetsen leveren een teststatistiek op die aangeeft hoe ver je data verwijderd zijn van de nulhypothese van de statistische toets. Vervolgens wordt een p-waarde berekend die uitdrukt hoe waarschijnlijk het is dat je data zouden voorkomen als de nulhypothese waar zou zijn.
De teststatistiek voor t-toetsen en regressieanalyses is de t-score. Hoewel de meeste statistische programma’s (zoals SPSS) automatisch de bijbehorende p-waarde voor de t-score berekenen, kun je de waarden ook opzoeken in een t-tabel, waarbij je de vrijheidsgraden en t-score gebruikt om de p-waarde te vinden.
De t-score die gepaard gaat met een p-waarde die kleiner is dan het significantieniveau alfa, wordt de kritische waarde van t, of t* genoemd.
Het aantal vrijheidsgraden is 38 (n – 1 voor elke groep). Als je dit getal opzoekt in een t-tabel of SPSS gebruikt, vind je een p-waarde die kleiner is dan 0.001.
Dit suggereert (net als het betrouwbaarheidsinterval) dat het zeer onwaarschijnlijk is dat je dit grote verschil in toetsscores van de steekproef zou tegenkomen als het daadwerkelijke verschil in toetsscores van de populatie 0 zou zijn.
Veelgestelde vragen
Citeer dit Scribbr-artikel
Als je naar deze bron wilt verwijzen, kun je de bronvermelding kopiëren of op “Citeer dit Scribbr-artikel” klikken om de bronvermelding automatisch toe te voegen aan onze gratis Bronnengenerator.
Merkus, J. (2021, 05 november). De t-verdeling (t-distribution) begrijpen | Met voorbeelden. Scribbr. Geraadpleegd op 24 februari 2026, van https://www.scribbr.nl/statistiek/t-verdeling/