Wat Is Kurtosis (Welving)? | Definitie & Voorbeelden

Vertaald op 9 augustus 2022 door Veronique Scharwächter. Oorspronkelijk gepubliceerd door Shaun Turney

Kurtosis (welving) is een maat voor de staartvormigheid (tailedness) van een verdeling. De staartvorm geeft aan hoe vaak uitschieters (outliers) voorkomen. Excess kurtosis is de staartvorm van een verdeling ten opzichte van een normale verdeling.

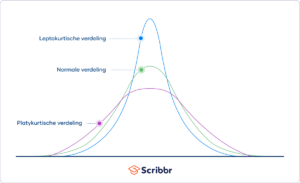
Verdelingen met een gemiddelde kurtosis (gemiddelde staarten) zijn mesokurtisch (mesokurtic).
Verdelingen met een lage kurtosis (dunne staarten) zijn platykurtisch (platykurtic).
Verdelingen met een hoge kurtosis (dikke staarten) zijn leptokurtisch (leptokurtic).

Staarten (tails) zijn de taps toelopende uiteinden aan weerszijden van een verdeling. Staarten vertegenwoordigen de waarschijnlijkheid of frequentie van waarden die extreem hoog of laag zijn in vergelijking met het gemiddelde. De staarten geven dus aan hoe vaak uitschieters voorkomen.

Voorbeeld: Soorten kurtosis

Let op

Kurtosis en skewness (scheefheid) zijn beide belangrijke maten voor de vorm van een verdeling. Skewness zegt iets over de scheefheid (asymmetrie) van de verdeling, terwijl kurtosis iets zegt over de welving (staartdikte) van de verdeling.

Soorten kurtosis

Verdelingen kunnen worden ingedeeld in drie groepen op basis van hun kurtosis:

	Categorie
	Platykurtisch	Mesokurtisch	Leptokurtisch
Staartvormigheid	Dunne staartvorm	Gemiddelde staartvorm	Dikke staartvorm
Frequentie uitschieters	Laag	Gemiddeld	Hoog
Kurtosis	Laag (< 3)	Matig (3)	Hoog (> 3)
Excess kurtosis	Negatief	0	Positief
Voorbeeld verdeling	Uniform	Normaal	Laplace

Ontvang feedback op taal, structuur, lay-out en bronvermelding

Professionele Scribbr-editors kijken je scriptie na op:

Academisch taalgebruik
Onduidelijke zinnen
Grammaticale fouten
Interpunctie
Verboden woorden

Bekijk het voorbeeld

Wat is een platykurtische verdeling?

Een platykurtische verdeling (platykurtic distribution) heeft een dunne staartvorm, wat betekent dat uitschieters niet vaak voorkomen.

Platykurtische verdelingen hebben minder kurtosis dan een normale verdeling. Oftewel, ze hebben:

Een kurtosis van minder dan 3
Een excess kurtosis van minder dan 0 (negatief)

Platykurtosis wordt soms ook wel negatieve kurtosis genoemd, omdat de excess kurtosis negatief is.

Let op

Het woord “platy” in “platykurtosis” komt van het Griekse woord platús, dat vlak betekent. Dit klopt echter niet, want, hoewel veel platykurtische verdelingen een afgeplatte piek hebben, hebben sommige platykurtische verdelingen een puntige piek.

Statistici begrijpen inmiddels dat kurtosis een maat is voor staartvormigheid (tailedness) en niet voor piekvormigheid (peakedness).

Voorbeeld: Platykurtische verdeling

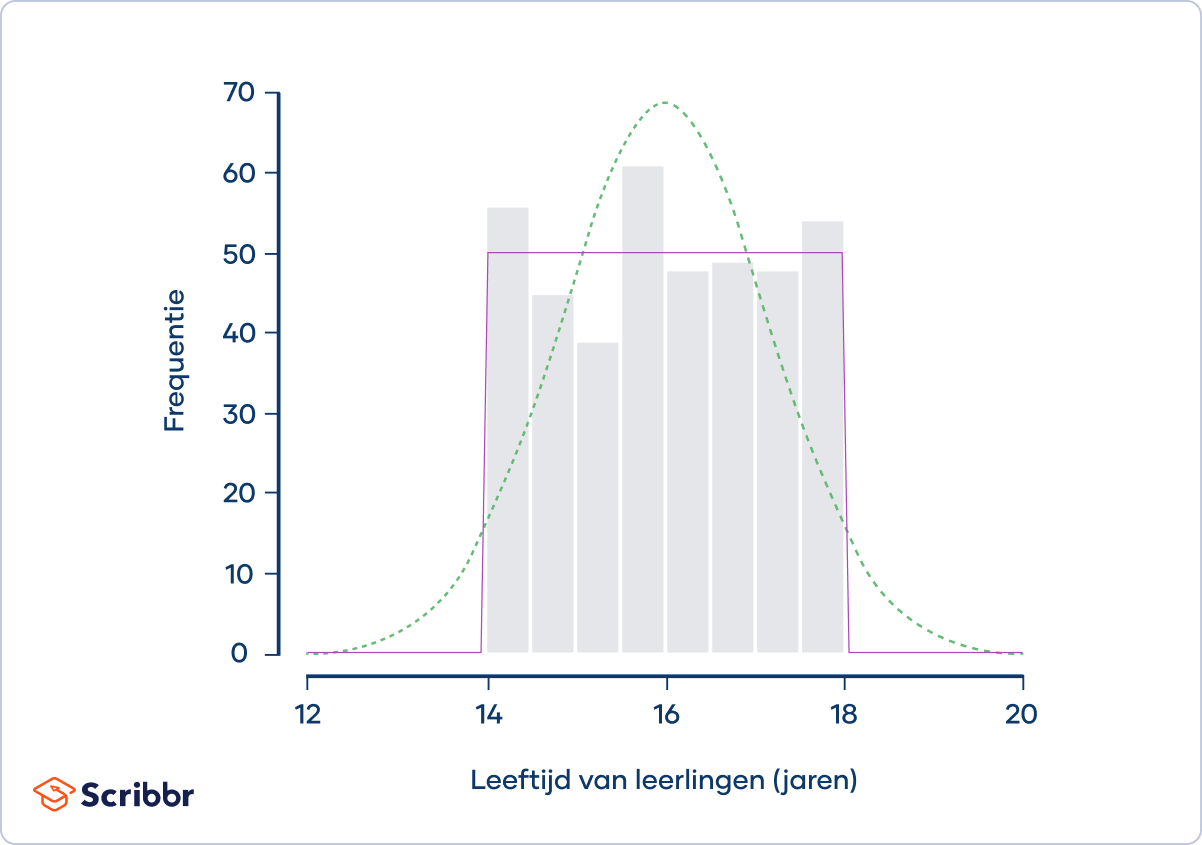
Een socioloog bestudeert het gebruik van sociale media door leerlingen van een kleine middelbare school. Er zitten 400 leerlingen op de school tussen de 14 en 18 jaar oud:

De frequentieverdeling (aangegeven door de grijze balken) volgt niet de normale verdeling (aangegeven door de gestippelde groene curve). In plaats daarvan volgt deze bij benadering een uniforme verdeling (aangegeven voor de paarse curve). Uniforme verdelingen zijn platykurtisch.

De socioloog berekent dat de kurtosis van de steekproef 1.78 is. De excess kurtosis is -1.22. Hij concludeert dat de verdeling platykurtisch is.

Platykurtische verdelingen hebben weinig uitschieters. Uniforme verdelingen, zoals de verdeling van de leeftijden van leerlingen, zijn extreme gevallen van platykurtische verdelingen, omdat uitschieters volledig afwezig zijn. Geen enkele leerling is jonger dan 14 jaar of ouder dan 18 jaar.

Let op

In de bovenstaande grafiek valt op dat aan de uiterste linker- en rechterkant van de verdeling (de staarten) de ruimte onder de paarse, uniforme curve dunner is dan de ruimte onder de groene, normale curve. Dat wordt bedoeld met “dunne staarten”.

Wat is een mesokurtische verdeling?

Een mesokurtische verdeling (mesokurtic distribution) heeft een gemiddelde staartvorm, zodat uitschieters niet erg vaak voorkomen, maar ook niet zeldzaam zijn.

Kurtosis wordt gemeten in verhouding tot een normale verdeling.

Normale verdelingen hebben een kurtosis van 3, dus elke verdeling met een kurtosis van ongeveer 3 is mesokurtisch.

Kurtosis wordt vaak beschreven als excess kurtosis, wat neerkomt op kurtosis – 3.

Excess kurtosis: kurtosis – 3

Aangezien normale verdelingen een kurtosis van 3 hebben, maakt excess kurtosis het vergelijken van de kurtosis van een verdeling met die van een normale verdeling nog makkelijker:

Normale verdelingen hebben een excess kurtosis van 0, dus elke verdeling met een excess kurtosis van ongeveer 0 is mesokurtisch.

Voorbeeld: Mesokurtische verdeling

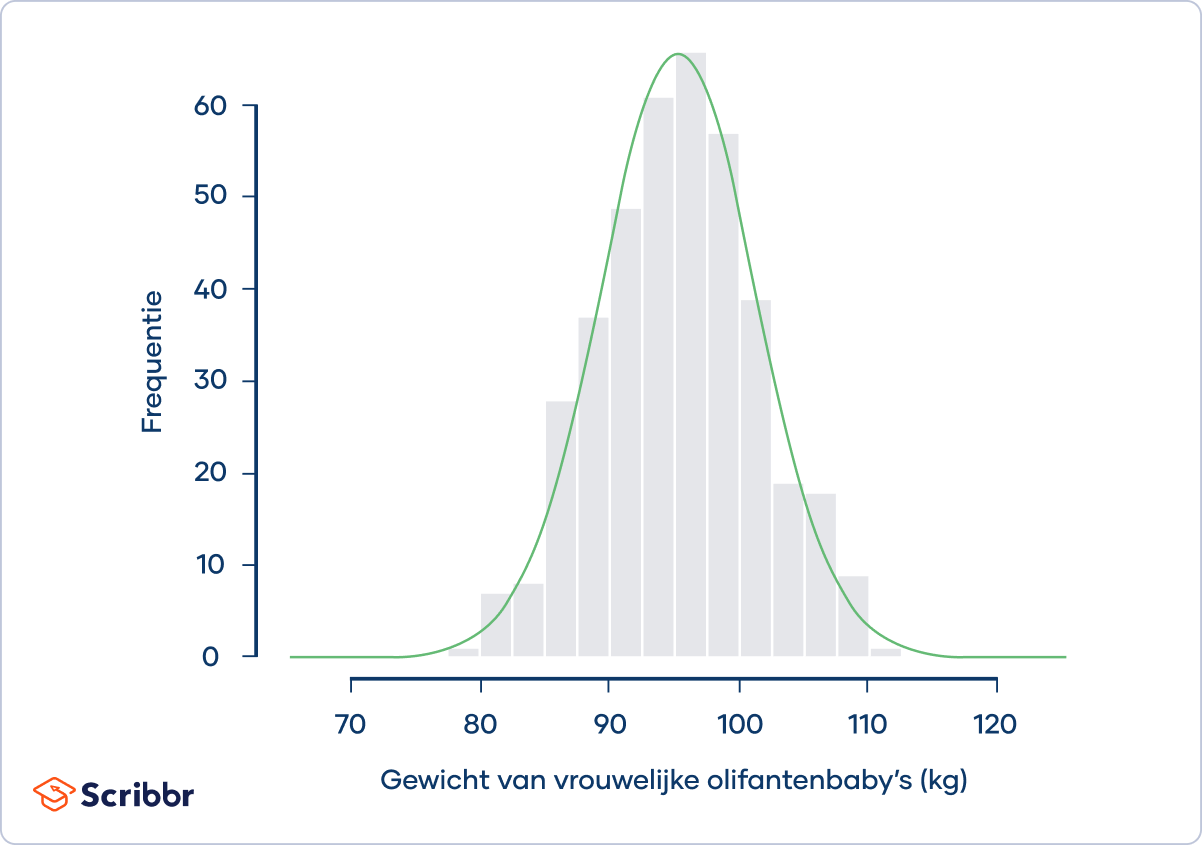
Gemiddeld weegt een vrouwtjesolifant bij geboorte maar liefst 95 kilogram (210 lbs). Stel dat een zoöloog geïnteresseerd is in de verdeling van het geboortegewicht van olifanten. Ze neemt contact op met dierentuinen en opvangcentra over de hele wereld en vraagt ze om hun data te delen. Zo verzamelt ze data over het geboortegewicht van 400 vrouwelijke babyolifantjes:

In de grafiek zie je dat de frequentieverdeling (aangegeven door de grijze balken) bij benadering een normale verdeling volgt (aangegeven door de groene curve). Normale verdelingen zijn mesokurtisch.

De zoöloog berekent de kurtosis van de steekproef. Ze vindt een kurtosis van 3.09 en een excess kurtosis van 0.09. Ze concludeert dat de verdeling mesokurtisch is.

Let op

Hoewel de kansverdeling van een populatie een kurtosis van precies 3 kan hebben, zijn echte data bijna altijd op zijn minst een beetje platykurtisch of leptopkurtisch.

Als een steekproef een kurtosis van ongeveer 3 heeft, kun je aannemen dat deze is getrokken uit een mesokurtische populatie.

Mesokurtische verdelingen hebben soms uitschieters en dit is ook zo voor het geboortegewicht van olifanten. Het komt af en toe voor dat er een vrouwtjesolifant wordt geboren met een gewicht van minder dan 81 kilogram (180 lbs) of meer dan 108 kilogram (240 lbs).

Wat is een leptokurtische verdeling?

Een leptokurtische verdeling (leptokurtic distribution) heeft een dikke staart, wat betekent dat er veel uitschieters zijn.

Leptokurtische verdelingen hebben meer kurtosis dan een normale verdeling. Oftewel, ze hebben:

Een kurtosis van meer dan 3
Een excess kurtosis van meer dan 0 (positief)

Leptokurtosis wordt ook wel positieve kurtosis genoemd, omdat de excess kurtosis positief is.

Let op

Het woord “lepto” in “leptokurtosis” komt van het Griekse woord leptós, dat smal betekent. Net als bij platykurtosis is dit een verkeerde benaming, omdat kurtosis niet om de piekvorm gaat, maar om de staartvorm.

Voorbeeld: Leptokurtische verdeling

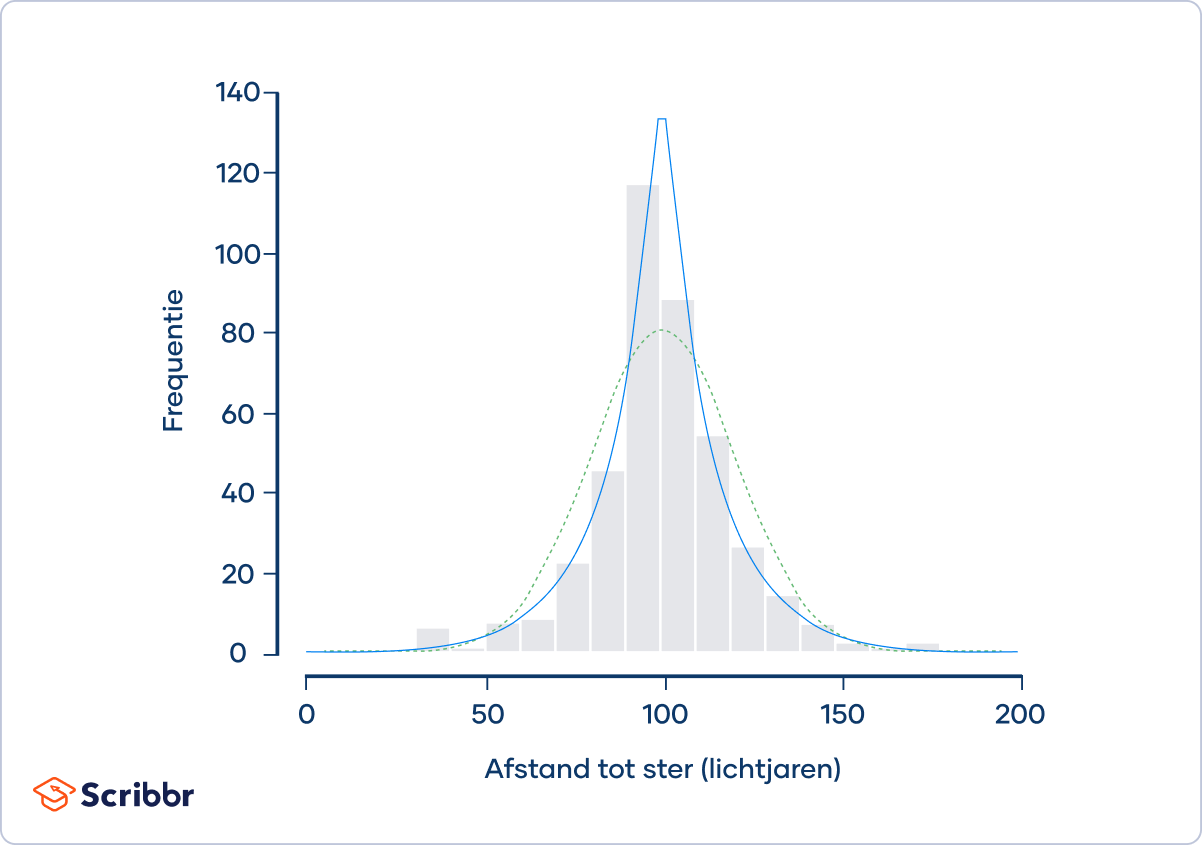
Stel je voor dat vier astronomen allemaal proberen de afstand te meten tussen de aarde en Nu2 Draconis A, een blauwe ster die deel uitmaakt van de Draco-constellatie. Alle vier de astronomen meten de afstand 100 keer. Ze voegen hun data samen in dezelfde dataset:

De frequentieverdeling (aangegeven door de grijze balken) volgt niet de normale verdeling (aangegeven door de gestippelde groene curve). In plaats daarvan volgt deze bij benadering een Laplaceverdeling (aangegeven door de blauwe curve). Laplaceverdelingen zijn leptokurtisch.

De astronomen berekenen dat de kurtosis van de steekproef 6.54 is. De excess kurtosis is 3.54. Ze concluderen dat de verdeling leptokurtisch is.

Leptokurtische verdelingen hebben frequente uitschieters. De verdeling van de metingen van de astronomen heeft meer uitschieters dan je zou verwachten bij een normale verdeling. Een aantal waarnemingen tonen extreme waarden van minder dan 50 lichtjaren of meer dan 150 lichtjaren afstand tot de ster.

Let op

Als je goed naar de bovenstaande grafiek kijkt, zie je dat aan de uiterste linker- en rechterkant van de verdeling (de staarten) de ruimte onder de blauwe, Laplacecurve iets dikker is dan de ruimte onder de groene, normale curve. Dat wordt bedoeld met “dikke staarten”.

Hoeveel fouten bevat jouw scriptie?

De taalexperts van Scribbr verbeteren gemiddeld 150 fouten per 1000 woorden. Benieuwd wat er precies wordt verbeterd? Verschuif de cursor van links naar rechts!

Scriptie nakijken op taal

Hoe bereken je kurtosis?

Wiskundig gesproken is kurtosis het gestandaardiseerde vierde moment van een verdeling. Momenten zijn een reeks metingen die iets zeggen over de vorm van de verdeling.

Momenten worden gestandaardiseerd door ze te delen door de standaarddeviatie die je verheft tot de juiste macht.

Kurtosis van een populatie

Onderstaande formule beschrijft de kurtosis van een populatie:

$\begin{equation*} \textup{kurtosis}=\tilde{\mu}_4=\dfrac{\mu_4}{\sigma^4} \end{equation*}$

Waarbij:

$\tilde{\mu}_4$ = het gestandaardiseerde vierde moment
$\mu_4$ = het niet-gestandaardiseerde centrale vierde moment
$\sigma$ = de standaarddeviatie

Kurtosis van een steekproef

De kurtosis van een steekproef is een schatting van de kurtosis van een populatie.

Het lijkt vanzelfsprekend om de kurtosis van een steekproef te berekenen als het vierde moment van de steekproef gedeeld door de standaarddeviatie tot de vierde macht. Dit leidt echter tot een vertekende schatting.

De formule voor de onvertekende schatting van de excess kurtosis bevat een langdurige correctie op basis van de steekproefgrootte:

$\begin{equation*}\textup{kurtosis}=\dfrac{n(n+1)}{(n-1)(n-2)(n-3)}\dfrac{\sum{(x_i-\bar{x})^4}}{(\sum{(x_i-\bar{x})^2})^2}-3\dfrac{(n-1)^2}{(n-2)(n-3)}\end{equation*}$

Waarbij:

$n$ = de steekproefgrootte
$x_i$ = de observaties van de variabele $x$
$\bar{x}$ = het gemiddelde van de variabele $x$

Het is erg tijdrovend om de kurtosis handmatig te berekenen. Daarom gebruiken de meeste mensen software om de kurtosis te berekenen. De KURT() functie in Excel berekent de kurtosis bijvoorbeeld op basis van bovenstaande formule.

Veelgestelde vragen over kurtosis

Wat zijn de drie soorten kurtosis?: De drie soorten kurtosis zijn:

Mesokurtosis: Een excess kurtosis van 0. Normale verdelingen zijn mesokurtisch.

Platykurtosis: Een negatieve excess kurtosis. Platykurtische verdelingen hebben een dunne staart, wat betekent dat ze weinig uitschieters hebben.

Leptokurtosis: Een positieve excess kurtosis. Leptokurtische verdelingen hebben een dikke staart, wat betekent dat ze veel uitschieters hebben.
Wat is een normale verdeling?: Er zijn twee parameters die bepalen hoe de normale verdeling eruitziet: het gemiddelde en de standaarddeviatie.

Binnen één standaarddeviatie ligt 68,2% van de observaties (34,1% + 34,1%), binnen twee standaarddeviaties 95,2% en binnen drie standaarddeviaties 99,6%.

De centrummaten (gemiddelde, modus en mediaan) hebben bij een normale verdeling dezelfde waarde.

De data zijn symmetrisch verdeeld, zonder skewness (zero skew).
Wat is het verschil tussen skewness en kurtosis?: Skewness en kurtosis zijn beide belangrijke maten voor de vorm van een verdeling.

Skewness (scheefheid) meet de asymmetrie van een verdeling.

Kurtosis (welving) meet de dikte van de staart van een verdeling ten opzichte van de normale verdeling.

Citeer dit Scribbr-artikel

Als je naar deze bron wilt verwijzen, kun je de bronvermelding kopiëren of op “Citeer dit Scribbr-artikel” klikken om de bronvermelding automatisch toe te voegen aan onze gratis Bronnengenerator.

Scharwächter, V. (2022, 09 augustus). Wat Is Kurtosis (Welving)? | Definitie & Voorbeelden. Scribbr. Geraadpleegd op 15 april 2024, van https://www.scribbr.nl/statistiek/kurtosis-uitgelegd/

Citeer dit artikel

Wat vind jij van dit artikel?

Je hebt al gestemd op dit artikel. Bedankt :-) Je stem is doorgevoerd :-) Bezig met het verwerken van je stem...

Veronique Scharwächter

Veronique heeft twee bachelors: één in Taal- en Cultuurstudies en één in Philosophy, Politics and Economics. Daarnaast heeft zij een boek geschreven over hoe filosofie je kan helpen in je studentenleven. Ze hoopt haar brede, interdisciplinaire kennis in te kunnen zetten om zo veel mogelijk studenten te helpen met het schrijven van hun scriptie.

Laat je scriptie nakijken op taal

Check je scriptie gratis op plagiaat

Literatuurlijst genereren volgens de APA-stijl

Scriptie nakijken & verbeteren

Plagiaat Checker

Bronnengenerator

Parafraseren

Spellingscontrole

Samenvatting maken

Wat Is Kurtosis (Welving)? | Definitie & Voorbeelden

Inhoudsopgave

Soorten kurtosis

Ontvang feedback op taal, structuur, lay-out en bronvermelding