Intervaldata verzamelen en analyseren | Met voorbeelden
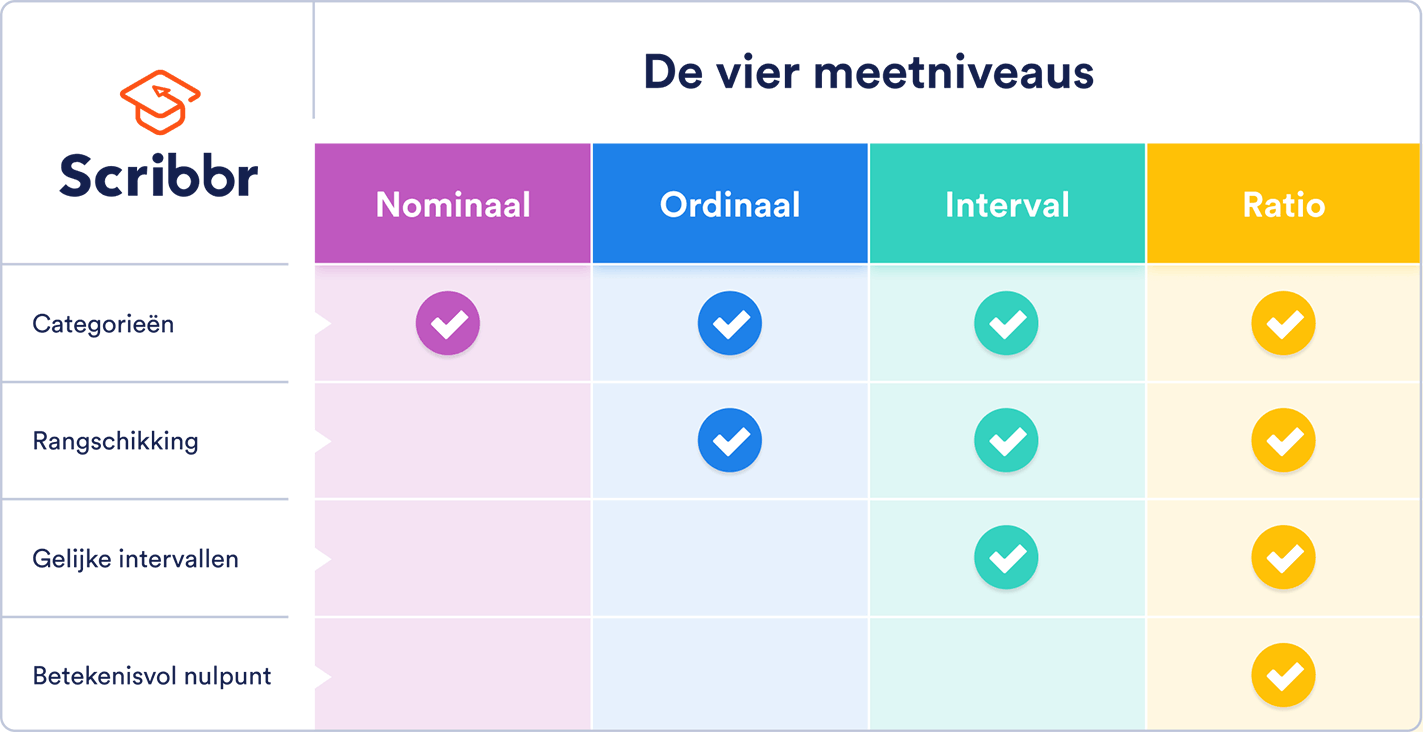
Intervaldata wordt gemeten op een numerieke schaal met gelijke afstanden tussen de aangrenzende waarden. Deze afstanden worden “intervallen” genoemd. Doordat de afstanden tussen de verschillende datapunten gelijk zijn, kun je bepaalde berekeningen uitvoeren.
Het verschil tussen interval- en ratiodata is dat een intervalschaal geen natuurlijk nulpunt kent. Bij een schaal op intervalniveau is het nulpunt willekeurig gekozen, en betekent het niet dat de variabele compleet afwezig is.
Zo is temperatuur (in graden Celsius) een intervalvariabele. Het nulpunt is willekeurig gekozen en 0 graden betekent het niet dat er helemaal geen temperatuur aanwezig is (of dat dit de koudst mogelijke temperatuur is). Tijd is daarentegen een ratiovariabele, omdat 0 minuten daadwerkelijk een betekenisvol nulpunt is (en het laagst mogelijke aantal).
De vier meetniveaus
Het intervalniveau is een van de vier meetniveaus. Deze niveaus geven aan hoe precies de data zijn verzameld. Hoe hoger het niveau, hoe complexer en preciezer de meting is.
Nominale en ordinale variabelen zijn categorisch, terwijl interval- en ratiovariabelen kwantitatief van aard zijn. Je kunt veel meer statistische toetsen gebruiken voor kwantitatieve data dan voor categorische data.
Interval versus ratio
Interval- en ratioschalen worden allebei gekenmerkt door gelijke intervallen tussen opeenvolgende waarden. Echter, ratioschalen hebben een betekenisvol, natuurlijk nulpunt, terwijl intervalschalen dit niet hebben.
Celsius en Fahrenheit zijn voorbeelden van intervalschalen. Ieder punt op deze schalen verschilt precies 1 graad van het vorige of volgende punt. Het verschil tussen 20 en 21 graden is exact hetzelfde als het verschil tussen 34 en 35 graden. Daarnaast zijn de nulpunten op deze schalen arbitrair: 0 graden Celsius of Fahrenheit is niet de laagst mogelijke temperatuur.
Aangezien er geen natuurlijk nulpunt is, kun je de scores niet vermenigvuldigen of door elkaar delen. Zo is 30°C niet twee keer zo warm als 15°C.
De temperatuurschaal voor Kelvin is wel een ratioschaal, omdat 0 het absolute nulpunt is. Niets is kouder dan 0 K. Daarom kun je deze waarden wel vermenigvuldigen of door elkaar delen: 20 K is twee keer zo heet als 10 K.
Voorbeelden van intervaldata
Psychologische concepten, zoals intelligentie, worden vaak gekwantificeerd tijdens het operationaliseren. De meeste testen die worden gebruikt hebben gelijke intervallen tussen scores, maar er zijn geen betekenisvolle nulpunten, omdat ze niet “nul intelligentie” of “nul persoonlijkheid” kunnen meten.
| Soort | Voorbeelden |
|---|---|
| Gestandaardiseerde test | IQ
CITO MMSE |
| Psychologische testen | Beck’s Depression Inventory
Raven’s Progressive Matrices Big Five personality trait test |
Om te bepalen of een schaal van ordinaal of intervalniveau is, kun je controleren of er gestandaardiseerde meeteenheden worden gebruikt, waarbij het verschil tussen twee waarden bekend is. Bijvoorbeeld:
- Interval: Een schaal om pijn te beoordelen van 0 (geen pijn) tot 10 (ergst mogelijke pijn).
- Ratio: Een schaal om pijn te beoordelen met de scores geen pijn, milde pijn, ernstige pijn, maximale pijn.
Data-analyse van intervaldata
Om een beeld te krijgen van je data, kun je eerst de volgende descriptieve statistieken verzamelen:
- De frequentieverdeling (absolute cijfers of percentages);
- De modus, mediaan of het gemiddelde om een beeld te krijgen van de centrale tendens;
- Het bereik, de standaarddeviatie en de variantie om de spreiding aan te geven.
Voor dit onderzoek verzamel je de SAT-scores van een groep van 59 scholieren uit Atlanta. De SAT-score kan variëren van 400 tot 1600.
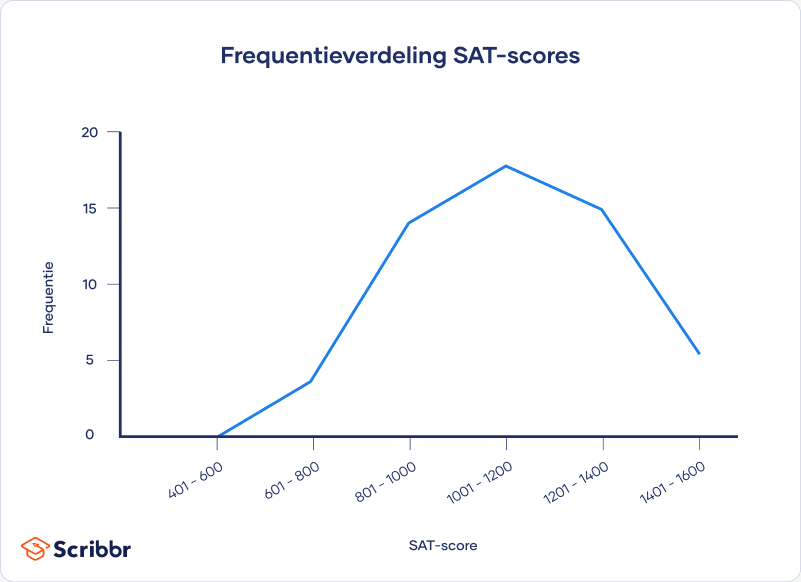
Verdeling
Tabellen en grafieken kunnen worden gebruikt om je data te organiseren en de verdeling van je data te visualiseren.
| SAT-score | Frequentie |
|---|---|
| 401 – 600 | 0 |
| 601 – 800 | 4 |
| 801 – 1000 | 15 |
| 1001 – 1200 | 19 |
| 1201 – 1400 | 16 |
| 1401 – 1600 | 5 |
Centrale tendens
De grafiek laat zien dat je data redelijk normaal verdeeld zijn. Er is geen sprake van een scheve verdeling, dus je kunt de drie meest gebruikte maten voor de centrale tendens gebruiken: de modus, de mediaan en het gemiddelde.
(n+1)/2 = (59+1)/2 = 30
De mediaan is de waarde op de 30e positie, en in dit geval is dat de waarde 1120.
⅀x = 65850
n = 59
⅀x/n = 65850/59 = 1116,1
Het gemiddelde wordt meestal beschouwd als de beste maat voor de centrale tendens, mits je data normaal zijn verdeeld. Dat komt doordat je voor de berekening van deze maat alle waarden in je dataset gebruikt, in tegenstelling tot bij de modus of de mediaan.
Spreiding
Het bereik (range), de standaarddeviatie en de variantie geven informatie over de spreiding van je data rond het gemiddelde. Het bereik is het makkelijkst te berekenen, maar de standaarddeviatie en variantie geven je betere informatie over de spreiding.
Bereik = 1500 – 620 = 880
s = 210,42
s2 = 44279,36
Statistische toetsen
Nu je een beeld hebt van je data, kun je de juiste statistische toets kiezen om je data te analyseren. Als je data normaal verdeeld zijn, kun je zowel voor parametrische als non-parametrische toetsen kiezen.
Parametrische toetsen hebben meer power dan non-parametrische toetsen en je kunt sterkere conclusies trekken op basis van je data. Je data moeten echter wel aan enkele eisen voldoen om parametrische toetsen te kunnen uitvoeren.
De volgende parametrische toetsen worden vaak gebruikt om hypothesen over intervaldata te toetsen.
| Doel | Steekproef of variabelen | Toets | Voorbeeld |
|---|---|---|---|
| Vergelijking van gemiddelden | 2 steekproeven | T-toets | Wat is het verschil in CITO-scores van studenten van twee verschillende basisscholen? |
| Vergelijking van gemiddelden | 3 of meer steekproeven | ANOVA | Wat is het verschil in CITO-scores van scholieren uit drie CITO-trainingsgroepen? |
| Correlatie | 2 variabelen | Pearson’s r | Hoe correleren CITO-scores met Entreetoets-scores? |
| Regressieanalyse | 2 variabelen | Enkelvoudige lineaire regressie | Wat is de invloed van het huishoudinkomen op CITO-scores van kinderen? |
Veelgestelde vragen
- Wat zijn de vier meetniveaus?
-
Meetniveaus laten zien hoe precies variabelen worden gemeten. Er zijn vier meetniveaus (of meetschalen) die van laag naar hoog kunnen worden gerangschikt.
- Nominaal: De data kunnen alleen worden gecategoriseerd (geen rangorde).
- Ordinaal: De data kunnen worden gecategoriseerd en gerangschikt.
- Interval: De data kunnen worden gecategoriseerd en gerangschikt en er zijn gelijke intervallen tussen de categorieën.
- Ratio: De data kunnen worden gecategoriseerd en gerangschikt, de intervallen zijn gelijk, en er is een absoluut of betekenisvol nulpunt.
- Hebben likertschalen een ordinaal of intervalmeetniveau?
-
Je data kunnen twee meetniveaus hebben: ordinaal of interval. De data-analysemethode is afhankelijk van het meetniveau van de data.
- data van de individuele likertvragen zijn ordinaal.
- data van de totale likertschaal worden beschouwd als intervaldata.
Bij ordinale schalen zijn de verschillen tussen de antwoordopties niet gelijk verdeeld of onbekend. Zo weet je bijvoorbeeld niet zeker of het verschil tussen “Helemaal mee oneens” en “oneens” even groot is als het verschil tussen “oneens” en “neutraal”.
Bij intervalschalen zijn deze verschillen tussen antwoordopties wel gelijk. Zo is het verschil tussen “1” en “2” bijvoorbeeld net zo groot als het verschil tussen “2” en “3”.
De data van de totale likertschaal worden vaak gezien als intervaldata, omdat het een totaalscore is waarbij scores van vier of meer vragen bij elkaar zijn opgeteld.
Citeer dit Scribbr-artikel
Als je naar deze bron wilt verwijzen, kun je de bronvermelding kopiëren of op “Citeer dit Scribbr-artikel” klikken om de bronvermelding automatisch toe te voegen aan onze gratis Bronnengenerator.
Merkus, J. (2021, 06 augustus). Intervaldata verzamelen en analyseren | Met voorbeelden. Scribbr. Geraadpleegd op 9 december 2024, van https://www.scribbr.nl/statistiek/interval/
