Descriptieve of beschrijvende statistiek | Uitleg & Voorbeelden

Met descriptieve of beschrijvende statistiek orden je de data en vat je de kenmerken van je dataset samen. Een dataset is een verzameling reacties of observaties van een steekproef of een hele populatie.

Bij kwantitatief onderzoek begin je aan je statistische analyse na afronding van de dataverzameling. Bij de eerste stap beschrijf je de kenmerken van de antwoorden, zoals het gemiddelde van een variabele (bijvoorbeeld leeftijd), of de relatie tussen twee variabelen (bijvoorbeeld tussen leeftijd en creativiteit).

Bij de volgende stap kijk je naar toetsende of inferentiële statistieken, die je helpen beslissen of de data je hypothese bevestigen en of het resultaat generaliseerbaar is naar een grotere populatie.

Soorten beschrijvende statistieken

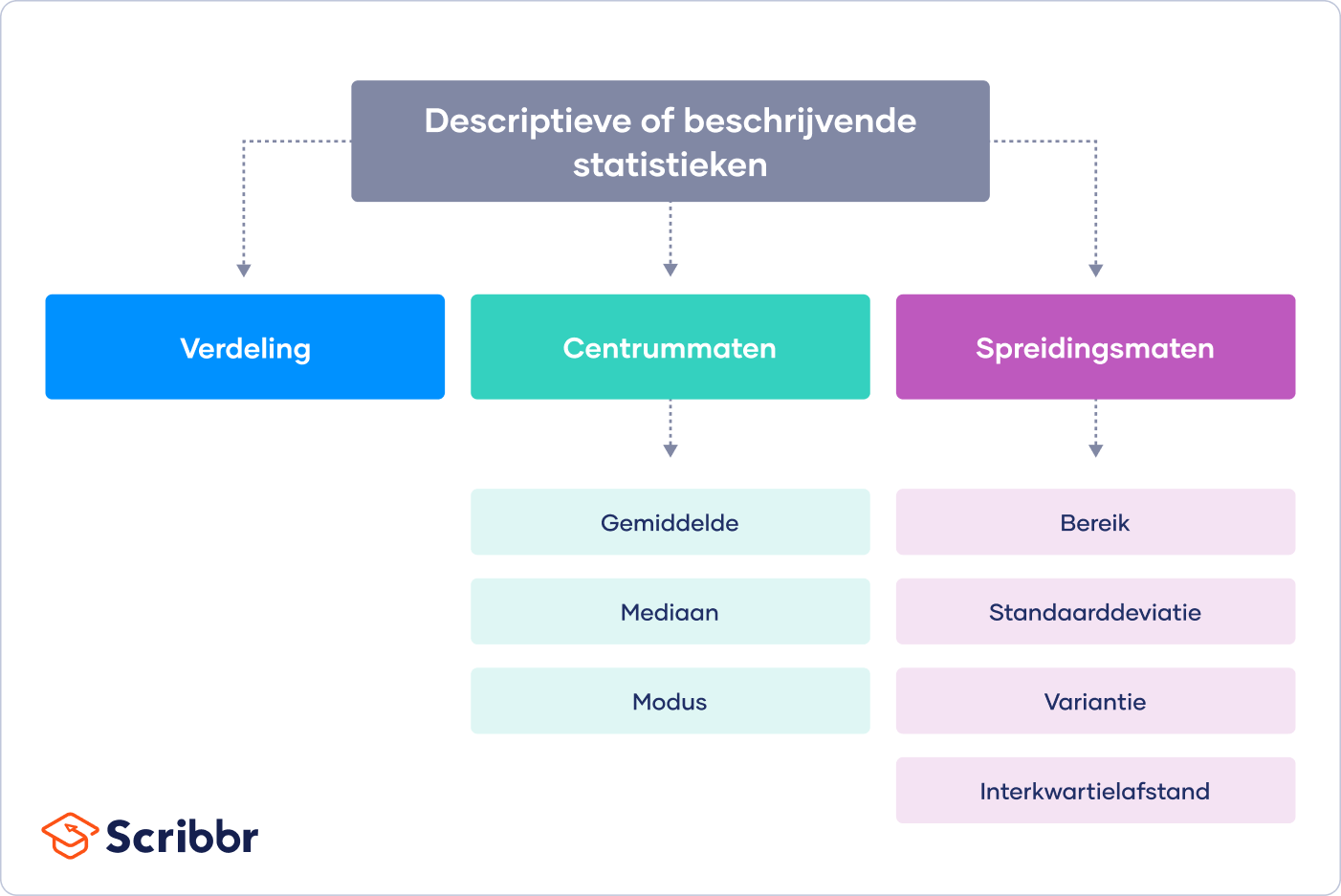
Er zijn drie belangrijke soorten beschrijvende statistieken:

• De verdeling heeft betrekking op de frequentie voor iedere waarde.
• De centrale tendens gaat over de gemiddelden voor de waarden.
• De spreiding (of variabiliteit) heeft te maken met de mate waarin waarden in de dataset verspreid zijn.

Je kunt deze statistieken toepassen op één variabele tegelijk bij een univariate analyse, of op twee of meer variabelen in het geval van een bivariate of multivariate analyse.

Wie helpt jou met nakijken?

Betrouwbare hulptroepen vinden is niet makkelijk...

• Familie
• Vrienden
• Studiegenoten
• Scribbr

We staan altijd voor je klaar

Frequentieverdeling (frequency distribution)

Een dataset bestaat uit een verzameling van waarden of scores. Je kunt de frequentie waarmee iedere waarde voorkomt samenvatten in een tabel, bijvoorbeeld door absolute cijfers of percentages te gebruiken.

Centrummaten

Je schat het centrum of midden van een dataset met behulp van centrummaten (measures of central tendency). Je kunt het centrum vinden met behulp van het gemiddelde, de mediaan en de modus.

In deze voorbeelden laten we zien hoe je de drie centrummaten handmatig kunt berekenen aan de hand van de eerste zes antwoorden op onze enquête. In de meeste gevallen kan de tool waarmee je je dataset analyseert (zoals Excel of SPSS) deze maten automatisch voor je berekenen.

Spreidingsmaten

Spreidingsmaten (measures of variability) laten zien in welke mate de antwoorden verspreid zijn rondom het gemiddelde. Het bereik, de standaarddeviatie en variantie zeggen alle drie iets over de spreiding.

Bereik

Het bereik of de spreidingsbreedte (range) geeft je een idee van hoe ver de meest extreme antwoordopties uit elkaar liggen. Om het bereik te vinden, trek je de laagste waarde van de hoogste waarde af.

Standaarddeviatie of standaardafwijking

De standaarddeviatie (ook wel standaardafwijking, standard deviation of s) is de gemiddelde hoeveelheid variabiliteit in je dataset. Deze maat vertelt je hoe ver iedere score gemiddeld van het gemiddelde verwijderd is. Des te groter de standaarddeviatie, des te meer variabel je dataset is.

Er zijn zes stappen om de standaarddeviatie te berekenen (al kun je deze maat in Excel of SPSS automatisch laten berekenen).

1. Maak een lijst van alle scores en vind het gemiddelde.
2. Trek het gemiddelde af van iedere score om de afstand (afwijking) tot het gemiddelde te berekenen.
3. Bereken voor iedere afwijking het kwadraat.
4. Tel alle gekwadrateerde afwijkingen bij elkaar op.
5. Deel de som van de gekwadrateerde afwijkingen door N – 1.
6. Trek de wortel van het gevonden nummer bij stap 5.

Variantie

De variantie (variance) is het gemiddelde van de kwadratische afwijkingen van het gemiddelde. Deze maat zegt iets over de mate van spreiding in een dataset. Des te meer spreiding er is, des te groter is de variatie in relatie tot het gemiddelde.

Om de variantie te berekenen, neem je het kwadraat van de standaarddeviatie. Het symbool voor variantie is s².

Hoeveel fouten bevat jouw scriptie?

De taalexperts van Scribbr verbeteren gemiddeld 150 fouten per 1000 woorden. Benieuwd wat er precies wordt verbeterd? Verschuif de cursor van links naar rechts!

Scriptie nakijken op taal

Univariate beschrijvende statistieken

Univariate beschrijvende statistieken richten zich op slechts één variabele tegelijk. Het is belangrijk om gegevens voor iedere variabele afzonderlijk te onderzoeken met behulp van meerdere maten voor verdeling, centrale tendens en spreiding. Je kunt programma’s als SPSS en Excel gebruiken om deze eenvoudig te berekenen.

Als je enkel het gemiddelde gebruikt als centrummaat, kan je beeld van het “midden” van de dataset vertekend zijn door extreme waarden (uitbijters of outliers). De mediaan en modus zijn hier minder gevoelig voor.

Ook het bereik is gevoelig voor extreme waarden, en daarom is het belangrijk om ook de standaarddeviatie en variantie te bepalen om een beeld te krijgen van de spreiding.

Bivariate beschrijvende statistieken

Als je data hebt verzameld voor meer dan één variabele, kun je bivariate of multivariate beschrijvende statistieken gebruiken om te onderzoeken of er relaties bestaan tussen je variabelen.

Bij een bivariate analyse kijk je naar de frequentie en spreiding van twee variabelen tegelijkertijd, om te bepalen of ze samen variëren. Je kunt ook de centrale tendens van beide variabelen bekijken voordat je verdere statistische analyses uitvoert.

Multivariate analyse is hetzelfde als bivariate analyse, maar dan met meer dan twee variabelen.

Kruistabellen

In een kruistabel (contingency table) laat iedere cel de kruising tussen twee variabelen zien. In de meeste gevallen zet je een onafhankelijke variabele (zoals leeftijdscategorie) in de kolommen (verticaal) en een afhankelijke variabele (zoals activiteit) in de rijen (horizontaal). In een kruistabel kun je de relatie tussen variabelen zien.

Het is makkelijker om een kruistabel te interpreteren als de onbewerkte gegevens (ruwe data) worden omgezet in percentages. Hierdoor kun je alle rijen met elkaar vergelijken. Als je percentages gebruikt voor je kruistabel, voeg je een N toe voor iedere onafhankelijke variabele.

Uit deze tabel blijkt beter dat vergelijkbare percentages kinderen en volwassenen meer dan 17 keer per jaar naar een bibliotheek gingen. Ook blijkt dat kinderen over het algemeen tussen de 5 en 8 keer per jaar gingen, en volwassenen tussen de 13 en 16 keer.

Scatterplots

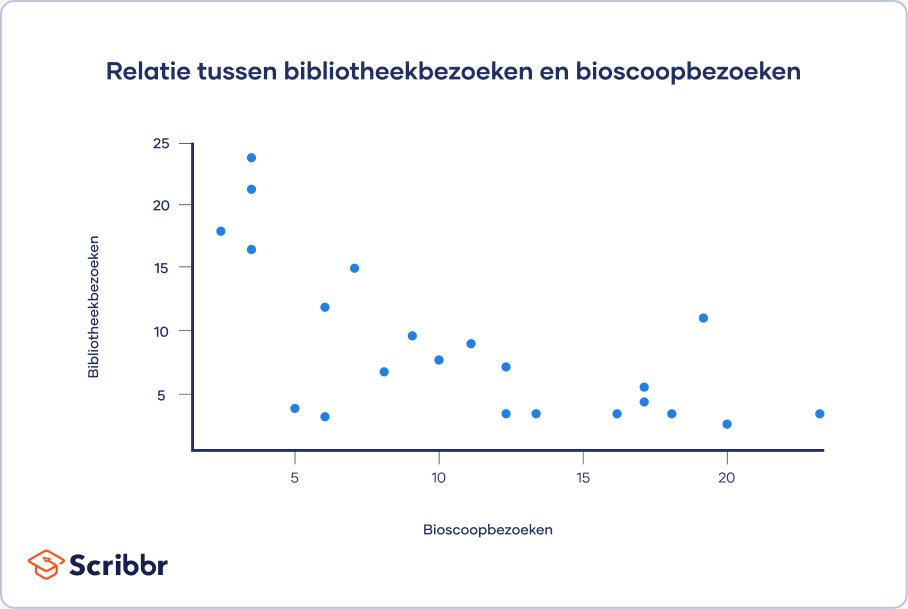
Een scatterplot (ook wel spreidingsgrafiek genoemd) is een grafiek die de relatie tussen twee of drie variabelen laat zien. De grafiek vormt een visuele weergave van de sterkte van een relatie.

In een scatterplot plot je een variabele op de x-as en een andere op de y-as. Ieder datapunt vormt een punt in de grafiek.

Veelgestelde vragen

Wat is het verschil tussen beschrijvende en toetsende statistiek?

Met beschrijvende statistiek (ook wel descriptieve statistiek genoemd) vat je de kenmerken van een dataset samen. Met toetsende statistiek (ook wel inferentiële of verklarende statistiek genoemd) toets je een hypothese of bepaal je of je data generaliseerbaar zijn naar een bredere populatie.

Wat zijn de drie belangrijkste beschrijvende statistieken?

De drie belangrijkste beschrijvende statistieken hebben betrekking op de frequentieverdeling, centrale tendens en variabiliteit van de dataset.

• Verdeling (distribution) verwijst naar de frequentie waarmee bepaalde antwoorden voorkomen.
• Centrummaten (measures of central tendency) geven je het gemiddelde voor iedere vraag.
• Spreidingsmaten (measures of variability) laten je de mate van spreiding in de dataset zien.

Wat is het verschil tussen univariate, bivariate en multivariate beschrijvende statistieken?

• Univariate statistieken vatten één variabele per keer samen.
• Bivariate statistieken vergelijken twee variabelen.
• Multivariate statistieken vergelijken drie of meer variabelen.

Wat is de standaarddeviatie?

De standaarddeviatie (standard deviation of s) is de gemiddelde hoeveelheid variabiliteit in je dataset. Deze maat vertelt je hoe ver iedere score gemiddeld van het gemiddelde verwijderd is. Des te groter de standaarddeviatie, des te meer variabel je dataset is.