Aannames bij Statische Toetsen | Homoscedasticiteit, Lineariteit
Bij het uitvoeren van statistische toetsen zoals een regressieanalyse, t-toets of ANOVA worden vaak verschillende statistische aannames gedaan. Het is belangrijk om deze aannames te testen, want pas als deze kloppen kun je de juiste conclusies trekken.
In dit artikel leggen we de betekenis van de meest voorkomende aannames uit en laten we zien hoe je deze kunt testen.
Aanname 1: Lineair verband tussen variabelen
Bij het uitvoeren van een lineaire regressie is het belangrijk dat het verband tussen de verklarende variabele en de afhankelijke variabele lineair is. Dit betekent dat voor zowel lage als hoge waardes van de verklarende variabele de invloed gelijk is.
Voorbeeld:
De verklarende variabele lengte beïnvloedt de afhankelijke variabele gewicht. Een lineair verband betekent dat het gewicht net zoveel toeneemt als iemand van 150 cm naar 160 cm lengte groeit als van 180 cm naar 190 cm.
Testen voor een lineair verband
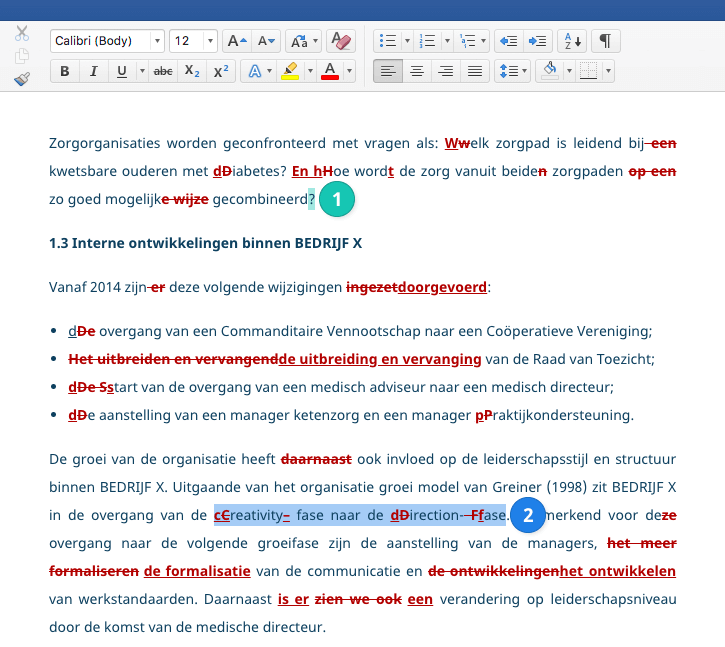
Je kunt het beste een spreidingsdiagram gebruiken om te analyseren of twee variabelen een lineair verband hebben. Als er een rechte lijn te trekken is door de punten, dan is er sprake van een lineair verband.
In SPSS maak je een spreidingsdiagram door te klikken op ‘Graphs’ → ‘Chart Builder’ en vervolgens ‘scatterplot’ te selecteren.
In het spreidingsdiagram aan de linkerkant is een rechte lijn door de puntenwolk te trekken: de invloed van lengte op gewicht is constant en er is dus sprake van een lineair verband.
In het spreidingsdiagram aan de rechterkant is er geen lineair verband. De invloed van gemiddeld inkomen op levensverwachting lijkt af te nemen naarmate het gemiddeld inkomen groter wordt.
Wat moet je doen als er geen lineair verband is?
Wanneer er geen lineair verband is, kun je het kwadraat of het logaritme van een variabele opnemen in de regressie. Dit doe je door de variabele te transformeren.
Het voordeel hiervan is dat het effect van de verklarende op de afhankelijke variabele beter geschat zal worden, maar de interpretatie van de regressiecoëfficiënten is wel wat lastiger.
Voorbeeld:
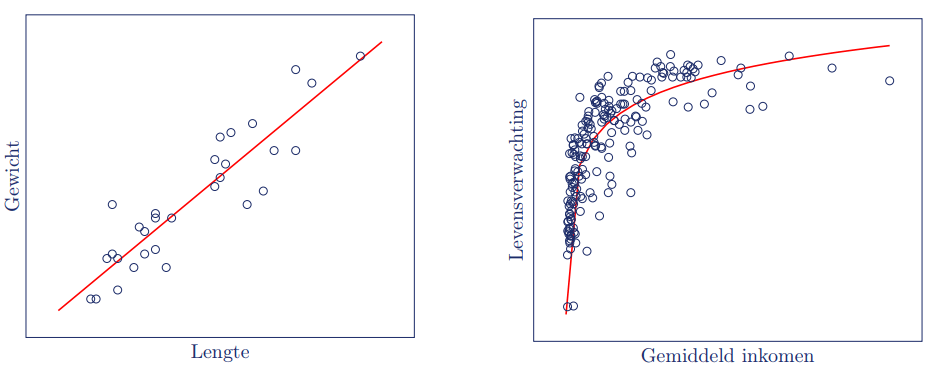
In het diagram aan de linkerkant is duidelijk dat het verband tussen inkomen en levensverwachting niet lineair is. Door een log-transformatie toe te passen op de inkomensdata, is te zien dat er wel een lineair effect is van verdubbeling van het inkomen op de levensverwachting.
Aanname 2: willekeurige steekproef
Bij het uitvoeren van onderzoek is het gebruikelijk om door middel van een steekproef data te verzamelen. De resultaten uit de steekproef wil je dan generaliseren naar de hele populatie.
Om dit te kunnen doen is het belangrijk dat je steekproef willekeurig is en dezelfde kenmerken heeft als de populatie.
Voorbeeld:
Je wil uitspraken doen over de lengte van de gemiddelde Nederlander. Wanneer je steekproef alleen uit basketballers bestaat dan zal dit een verkeerd beeld geven.
Onafhankelijke observaties
Naast het feit dat de respondenten willekeurig gekozen zijn, is het ook belangrijk dat de observaties onafhankelijk van elkaar zijn. Dit betekent dat de ene observatie de andere niet mag beïnvloeden.
Voorbeeld:
Je hebt respondenten die familie van elkaar zijn. Hun lengte hangt met elkaar samen waardoor ze dus niet onafhankelijk zijn.
In tegenstelling tot de andere aannames in dit artikel is de aanname van een willekeurige steekproef niet te testen. In plaats daarvan moet je kritisch kijken naar hoe je je steekproef hebt uitgevoerd.
Aanname 3: multicollineariteit
Wanneer er een sterk lineair verband is tussen verklarende variabelen, spreekt men van multicollineariteit.
Multicollineariteit kan ertoe leiden dat de regressiecoëfficiënten in je regressiemodel slechter worden geschat. De verklarende variabelen voorspellen elkaar dan en daardoor wordt er geen extra variantie verklaard in het regressiemodel.
Voorbeeld:
Je voegt zowel lengte in centimeters als lengte in inches toe als verklarende variabelen aan je regressievergelijking. Deze twee variabelen voorspellen elkaar, aangezien lengte in centimeters 2,54 maal de lengte in inches is, en zijn dus perfect lineair gecorreleerd. Er kunnen dan geen twee regressiecoëfficiënten worden berekend.
Ook een combinatie van verschillende variabelen mag niet hetzelfde zijn als een andere variabele. Dit is bijvoorbeeld het geval voor eindexamen-, schoolexamen-, en eindcijfers op de middelbare school, aangezien het eindcijfer het gemiddelde is van de andere twee.
Testen voor multicollineariteit
Bij het uitvoeren van regressieanalyse in SPSS kun je onder Statistics ‘Collinearity diagnostics’ aanvinken. In de output verschijnt dan de VIF (Variance Inflation Factor).
Een vuistregel is dat er vanaf een VIF van vijf een probleem is voor het schatten van de regressiecoëfficiënt van de betreffende variabele. De VIF-waarde is alleen belangrijk voor de verklarende variabelen in je model. Bij controlevariabelen is een hoge VIF geen probleem.
Wat moet je doen bij multicollineariteit?
Wanneer er sprake is van multicollineariteit kan het verstandig zijn om de gecorreleerde variabelen te combineren tot één overkoepelend begrip. Je kunt hiervoor Cronbach’s alpha gebruiken of een factoranalyse uitvoeren.
Aanname 4: exogeniteit
Exogeniteit betekent dat de afhankelijke variabele afhangt van de verklarende variabele en de foutterm. Het tegenovergestelde is endogeniteit en dat moet worden voorkomen wanneer je uitspraken wilt doen over het effect van variabele A op variabele B (causaliteit).
Het effect van de verklarende variabele op je afhankelijke variabele wordt geschat met de regressiecoëfficiënt. Wanneer er sprake is van endogeniteit, wordt de regressiecoëfficiënt verkeerd geschat.
Oorzaken van endogeniteit
Er bestaan drie oorzaken voor endogeniteit.
1. Weggelaten variabele
Er is een andere variabele die gecorreleerd is met de verklarende variabele en die ook invloed heeft op de afhankelijke variabele. Dit kan worden opgelost door deze variabele ook op te nemen in de regressievergelijking.
Voorbeeld:
Stel je probeert het aantal drenkelingen te verklaren met ijsverkoop, dan is temperatuur een weggelaten variabele. Een hogere temperatuur zorgt immers voor meer zwemmers en dus ook drenkelingen, maar is ook een voorspeller voor de ijsverkoop.
Wanneer het aantal drenkelingen voorspeld kan worden door alleen ijsverkoop, is de geschatte regressiecoëfficiënt hoger dan de werkelijke regressiecoëfficiënt.
2. Omgekeerde causaliteit
Wanneer de afhankelijke variabele ook de verklarende variabele beïnvloedt, dan is er sprake van omgekeerde causaliteit. Dit kan worden opgelost door zogenaamde instrumentele variabelen te gebruiken.
Voorbeeld:
Stel dat je criminaliteit probeert te verklaren met politie-inzet, dan is er duidelijk sprake van omgekeerde causaliteit, aangezien meer criminaliteit juist zorgt voor meer politie-inzet. Het effect van politie-inzet op criminaliteit wordt onderschat in een regressie zonder instrumentele variabelen.
3. Meetfouten in verklarende variabele
Wanneer een verklarende variabele niet betrouwbaar gemeten is, wordt de regressiecoëfficiënt dichter bij nul geschat dan die daadwerkelijk is. Het is belangrijk dat je betrouwbare data gebruikt.
Endogeniteit voorkomen
De beste manier om endogeniteit te voorkomen is door experimenteel onderzoek te doen, waarbij je zelf de verklarende variabele manipuleert.
Of er mogelijk sprake is van endogeniteit, kun je niet op basis van je data zeggen. Wel kun je kritisch kijken naar je conceptueel model. Ga na of de pijlen de juiste richting op wijzen en of er geen variabelen ontbreken die invloed hebben op zowel de verklarende als de afhankelijke variabele.
Aanname 5: homoscedasticiteit
Homoscedasticiteit houdt in dat de variantie van een variabele gelijk is voor meerdere groepen of dat de variantie van de foutterm gelijk is.
Bij het uitvoeren van een t-toets of ANOVA analyseer je de variantie tussen de meerdere groepen. Dit kan getoetst kan worden met Levene’s test.
Bij regressie moet de variantie van de foutterm gelijk zijn voor alle waarden van de verklarende variabele. Er mag dus niet meer of minder spreiding in de foutterm zijn voor grotere of lagere waarden van de verklarende variabele.
Bij heteroscedasticiteit wordt de regressiecoëfficiënt zuiver geschat, maar de significantie is onbetrouwbaar. Deze kan zowel over- als onderschat worden. De kans bestaat dus dat je de verkeerde conclusie trekt.
Heteroscedasticiteit in regressie
Het is verstandig een spreidingsdiagram te generen om te kijken of de variantie van de foutterm gelijk is. In SPSS klik je hiervoor bij het uitvoeren van je regressie op ‘Save’ en vink je onder ‘Predicted Values’ en ‘Residuals’ Unstandardized aan.
Dit creëert de nieuwe variabelen voorspelde waarde en foutterm. In een spreidingsdiagram plot je de foutterm op de y-as en de voorspelde waarde op de x-as.
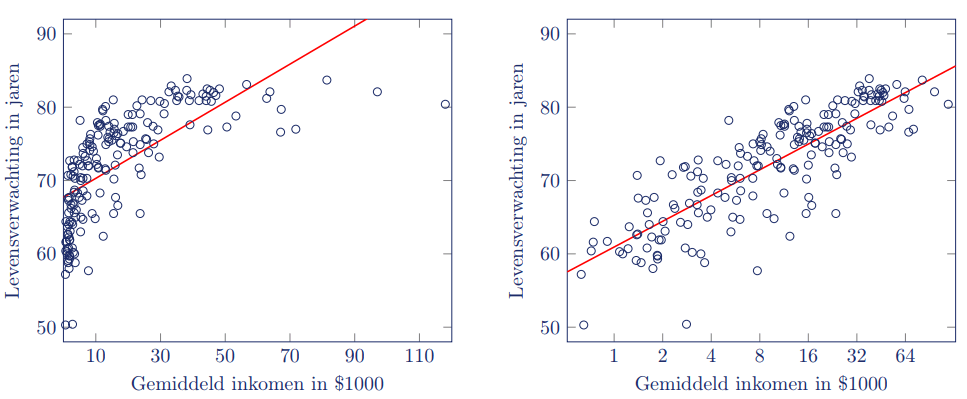
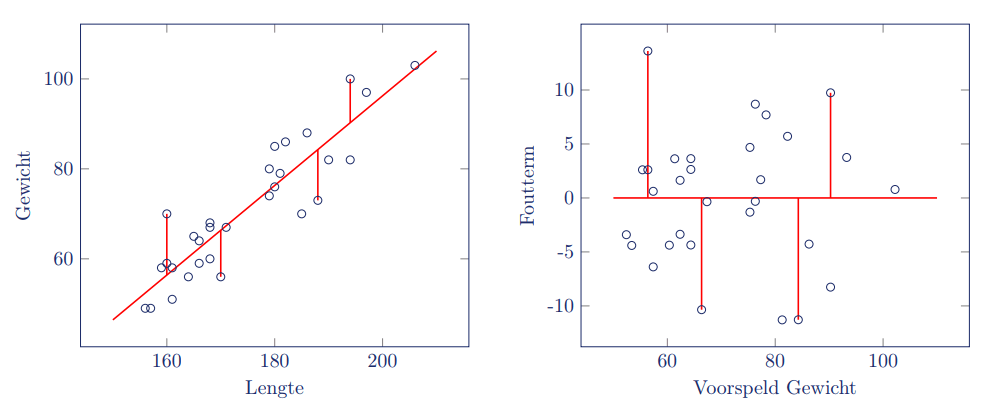
In de onderstaande spreidingsdiagrammen is te zien dat de observaties ongeveer even ver van de regressielijn liggen voor elke waarde van lengte, dus van heteroscedasticiteit lijkt geen sprake.
Wat moet je doen als er geen homoscedasticiteit is?
Wanneer er sprake is van heteroscedasticiteit kun je verschillende dingen proberen:
1. Transformeren van je variabele(n)
Het is mogelijk dat een transformatie van variabele(n) zorgt dat de heteroscedasticiteit verdwijnt. Heteroskedasticiteit kan namelijk ontstaan doordat er niet-lineaire verbanden zijn tussen de verklarende en afhankelijke variabele.
In dit geval is het noodzakelijk om de verklarende variabele te transformeren zodat er een lineair verband ontstaat waarbij de foutterm niet verandert voor hogere of lagere waarden van de verklarende variabele.
2. Gebruik een andere regressie
Naast de normale regressieanalyse is het ook mogelijk een gewogen (weighted) of gegeneraliseerde (generalized) regressie te gebruiken. Dit soort regressies veronderstellen geen homoscedasticiteit.
Bij een variabele die niet gemeten is op een interval- of ratioschaal, zoals het wél of niet slagen voor een tentamen, is logistische regressie een optie.
Veelgestelde vragen
- Wat is de assumptie van lineariteit?
-
Bij het uitvoeren van een lineaire regressie is het belangrijk dat het verband tussen de verklarende variabele en de afhankelijke variabele lineair is. Dit betekent dat voor zowel lage als hoge waarden van de verklarende variabele de invloed gelijk is.
Voorbeeld:
De verklarende variabele lengte beïnvloedt de afhankelijke variabele gewicht. Een lineair verband betekent dat het gewicht net zoveel toeneemt als iemand van 150 cm naar 160 cm lengte groeit als van 180 cm naar 190 cm. - Wat is multicollineariteit?
-
Als er een sterk lineair verband is tussen verklarende variabelen, spreek je van multicollineariteit.
Multicollineariteit kan ertoe leiden dat de regressiecoëfficiënten in je regressiemodel slechter worden geschat. De verklarende variabelen voorspellen elkaar dan en daardoor wordt er geen extra variantie verklaard in het regressiemodel.
Voorbeeld:
Je voegt zowel lengte in centimeters als lengte in inches toe als verklarende variabelen aan je regressievergelijking. Deze twee variabelen voorspellen elkaar, aangezien lengte in centimeters 2,54 maal de lengte in inches is, en zijn dus perfect lineair gecorreleerd. Er kunnen dan geen twee regressiecoëfficiënten worden berekend. - Wat is homoscedasticiteit?
-
Homoscedasticiteit houdt in dat de variantie van een variabele gelijk is voor meerdere groepen of dat de variantie van de foutterm gelijk is.
Bij het uitvoeren van een t-toets of ANOVA, analyseer je de variantie tussen de meerdere groepen. Dit kan getoetst kan worden met Levene’s test.
Bij regressie moet de variantie van de foutterm gelijk zijn voor alle waarden van de verklarende variabele. Er mag dus niet meer of minder spreiding in de foutterm zijn voor grotere of lagere waarden van de verklarende variabele.
Citeer dit Scribbr-artikel
Als je naar deze bron wilt verwijzen, kun je de bronvermelding kopiëren of op “Citeer dit Scribbr-artikel” klikken om de bronvermelding automatisch toe te voegen aan onze gratis Bronnengenerator.
van Heijst, L. (2023, 11 januari). Aannames bij Statische Toetsen | Homoscedasticiteit, Lineariteit. Scribbr. Geraadpleegd op 22 november 2024, van https://www.scribbr.nl/statistiek/aannames-statistiek/