T-tabel (Gratis Download) | Stappenplan & Voorbeelden

De t-tabel (t table) is een referentietabel met de kritieke waarden van t. De t-tabel wordt ook wel  Student’s t-tabel, t-verdelingstabel, t-score tabel, t-waarde tabel, of t-test tabel genoemd.

Een kritieke waarde van t bepaalt de drempel voor significantie voor statistische toetsen en de boven- en ondergrens van betrouwbaarheidsintervallen voor schattingen. De t-tabel wordt meestal gebruikt:

• Als je toetst of twee gemiddelden significant van elkaar verschillen (ongepaarde t-test, independent samples t test).
• Als je toetst of twee variabelen significant samenhangen (lineaire regressie of correlatie).
• Als je betrouwbaarheidsintervallen berekent (van gemiddelden of regressiecoëfficiënten).

Download de t-tabel

De kritieke waarden van t worden berekend aan de hand van de Student’s t-verdeling. Dit is de verdeling van teststatistiek t. Het is lastig om de kritieke waarden van t handmatig te berekenen. Daarom gebruiken de meeste mensen in plaats daarvan de t-tabel of computersoftware.

Student’s t-tabel voor eenzijdige en tweezijdige toetsen

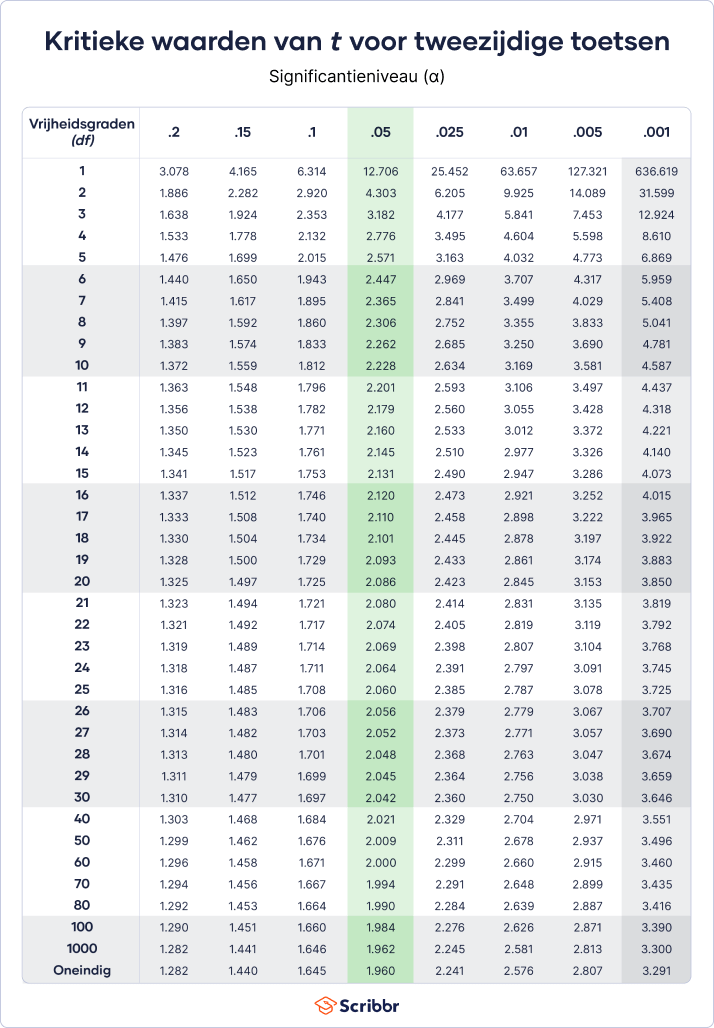
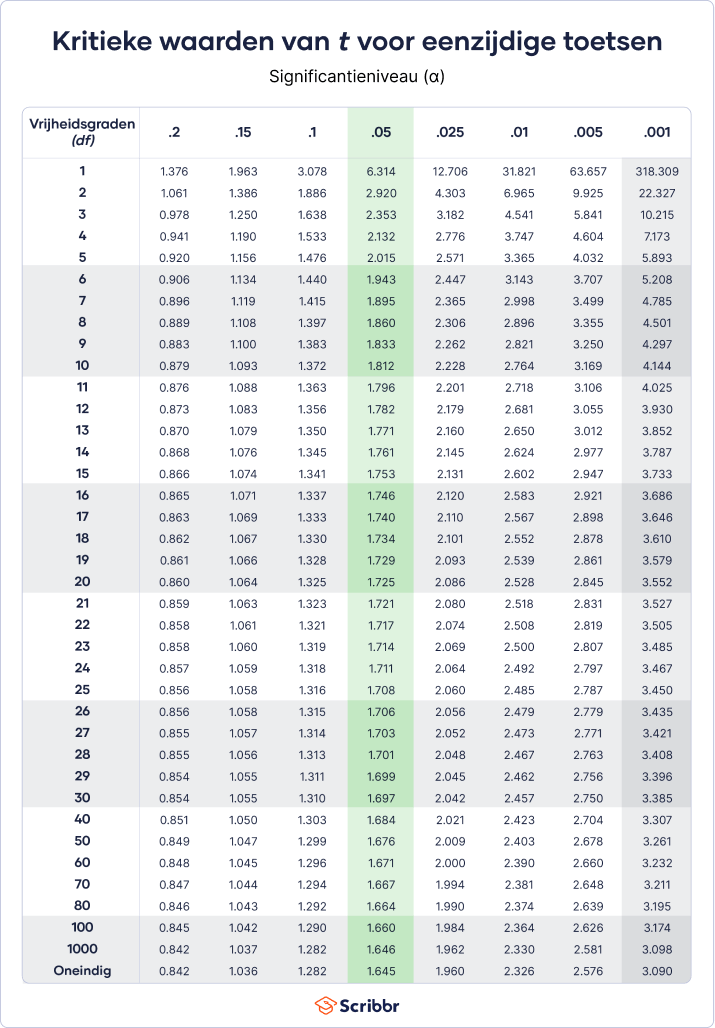
Gebruik onderstaande tabellen om de kritieke waarden van t te vinden. Er is een aparte tabel voor een eenzijdige t-toets (one-tailed t test) en een tweezijdige t-toets (two-tailed t test).

In de volgende sectie vind je een stappenplan waarin wordt uitgelegd hoe je de t-tabel gebruikt.

Download de t-tabel

Ontvang feedback op taal, structuur, lay-out en bronvermelding

Professionele Scribbr-editors kijken je scriptie na op:

• Academisch taalgebruik
• Onduidelijke zinnen
• Grammaticale fouten
• Interpunctie
• Verboden woorden

Bekijk het voorbeeld

Hoe gebruik je de t-tabel?

Als je een kritieke waarde van t moet vinden om een statistische toets uit te voeren of een betrouwbaarheidsinterval te berekenen, dan kun je onderstaand stappenplan volgen.

Stap 1: Kies eenzijdig of tweezijdig

Tweezijdige toetsen (two-tailed tests) worden gebruikt als de alternatieve hypothese geen richting heeft.

• Een niet-gerichte alternatieve hypothese stelt dat een populatieparameter (zoals een gemiddelde of regressiecoëfficiënt) niet gelijk (i.e., ≠) is aan een bepaalde waarde (zoals 0). Tweezijdige toetsen zijn geschikt voor de meeste studies.
• Voor het berekenen van een betrouwbaarheidsinterval kies je altijd voor een tweezijdige toets.

Eenzijdige toetsen (one-tailed tests) worden gebruikt als de alternatieve hypothese wel een richting heeft.

• Een gerichte alternatieve hypothese stelt dat een populatieparameter groter of kleiner is dan een bepaalde waarde.
• Je alternatieve hypothese heeft richting als deze woorden bevat zoals “groter dan”, “kleiner dan”, “stijgt”, “daalt”, of het “<” of “>” teken. Als deze woorden of symbolen er niet in voorkomen, heeft de hypothese waarschijnlijk geen richting.

Stap 2: Bereken de vrijheidsgraden

De vrijheidsgraden (df) van een statistiek worden berekend op basis van de steekproefgrootte (n). De formule die je hiervoor moet gebruiken hangt af van het soort toets dat je uitvoert.

Vrijheidsgraden (df) berekenen

Stap 3: Kies een significantieniveau

Over het algemeen is het significantieniveau (α) bijna altijd .05. In de te downloaden t-tabel is de kolom met ​​α = .05 gemarkeerd, omdat dit het meest gebruikte significantieniveau is.

In sommige gevallen kun je ervoor kiezen het risico op een Type I-fout te verkleinen door α te verhogen, of het risico op een Type II-fout te verkleinen door α juist te verlagen.

Als je een betrouwbaarheidsinterval berekent, kies je het significantieniveau op basis van het gewenste betrouwbaarheidsniveau:

α = 1 – betrouwbaarheidsniveau

Het meest voorkomende betrouwbaarheidsniveau is 95% (ook wel .95 als verhouding). Dit komt overeen met α = .05.

Stap 4: Vind de kritieke waarde van t in de t-tabel

Nu je hebt bepaald of je experiment eenzijdig of tweezijdig is en je weet wat je significantieniveau is en je vrijheidsgraden zijn, heb je alle informatie die nodig is om de t-tabel te gebruiken.

• Als je experiment tweezijdig is of als je een betrouwbaarheidsinterval berekent, gebruik dan de eerste tabel. Als de toets eenzijdig is, gebruik dan de tweede tabel.
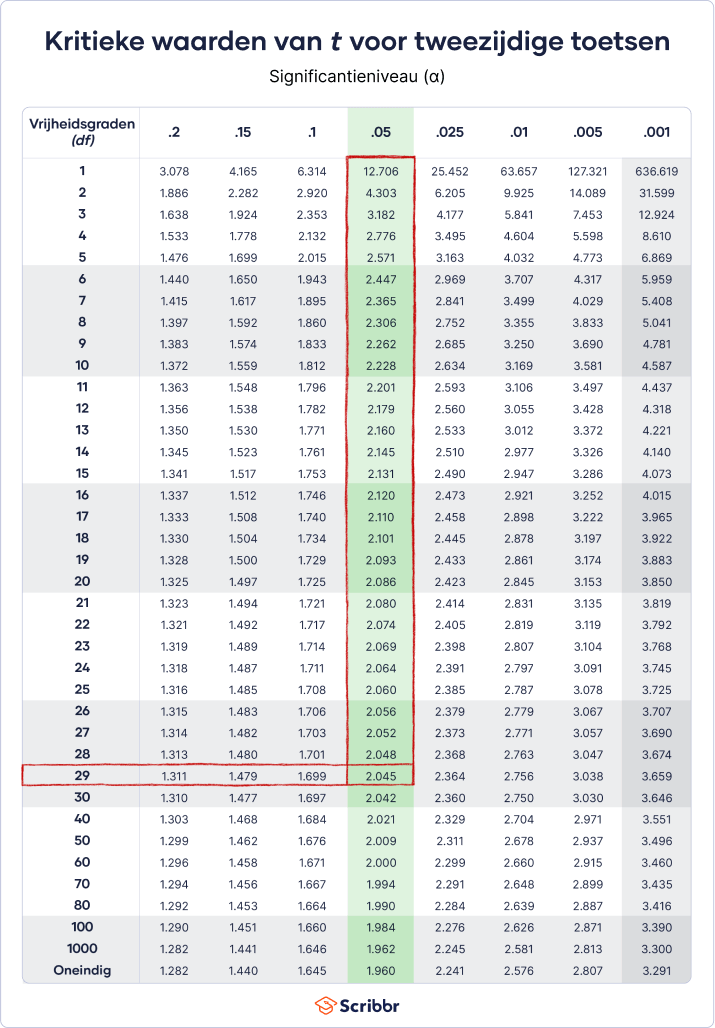
• De vrijheidsgraden (df) staan aan de linkerkant van de tabel. Zoek de tabelrij voor het aantal df dat je in stap 2 hebt berekend. Als je een df nodig hebt die niet in de rij staat, rond dan af naar het volgende kleinste getal (e.g., df = 46 lees je af bij df = 40).
• De significantieniveaus staan bovenaan de tabel vermeld. Zoek de kolom voor het significantieniveau dat je in stap 3 gekozen hebt. In de meeste gevallen zul je de gemarkeerde kolom gebruiken (α = .05).
• De kritieke waarde van t voor je toets vind je op de plek waar de rij en de kolom samenkomen.

Oefenvragen

Veelgestelde vragen over t-tabel

Hoe vind ik de kritieke waarde van t in R?

Je kunt de qt() functie gebruiken om de kritieke waarde van t te vinden in R. De functie geeft de kritieke waarde van t voor de eenzijdige toets. Als je de kritieke waarde van t voor een tweezijdige toets wilt, deel je het significantieniveau door twee.

Om de kritieke waarde van t voor een tweezijdige toets met df = 29 en α = .05 te berekenen, gebruik je de volgende functie:

qt(p = .025, df = 29)

Hoe vind ik de kritieke waarde van t in Excel?

Je kunt de T.INV() functie gebruiken om de kritieke waarde van t te vinden voor eenzijdige toetsen in Excel. Voor tweezijdige toetsen gebruik je de T.INV.2T() functie.

Om de kritieke waarde van t te berekenen voor een tweezijdige toets met df = 29 en α = .05, klik je op een lege cel en typ je:

=T.INV.2T(0.05,29)

Hoe toets ik een hypothese met behulp van de kritieke waarde van t?

Om een hypothese te toetsen met behulp van de kritieke waarde van t, volg je deze vier stappen:

1. Bereken de t-waarde en vrijheidsgraden van je steekproef.
2. Zoek de kritieke waarde van deze t-waarde in de t-tabel die hoort bij de juiste vrijheidsgraden.
3. Bepaalde of de (absolute) t-waarde groter is dan de kritieke waarde van t.
4. Verwerp de nulhypothese als de t-waarde van de steekproef groter is dan de kritieke waarde van t. Zo niet, dan verwerp je de nulhypothese niet.

Hoe bereken ik het betrouwbaarheidsinterval van een gemiddelde met de kritieke waarde van t?

Om een betrouwbaarheidsinterval van een gemiddelde te berekenen met behulp van de kritieke waarde van t, volg je deze vier stappen: 

1. Kies het significantieniveau op basis van het gewenste betrouwbaarheidsniveau. Het meest gebruikelijke betrouwbaarheidsniveau is 95%, wat overeenkomt met α = .05 in de tweezijdige t-tabel.
2. Zoek de kritieke waarde van t in de tweezijdige t-tabel.
3. Vermenigvuldig de kritieke waarde van t met .
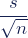4. Tel deze waarde bij het gemiddelde op om de bovengrens van het betrouwbaarheidsinterval te berekenen, en trek deze waarde van het gemiddelde af om de ondergrens van het betrouwbaarheidsinterval te berekenen.

Waarom heet de t-verdeling ook de Student’s t-verdeling?

De t-verdeling werd voor het eerst beschreven door statisticus William Sealy Gosset onder het pseudoniem “Student”.