Hoe voorkom je Type I- en Type II-fouten? | Uitleg & voorbeelden

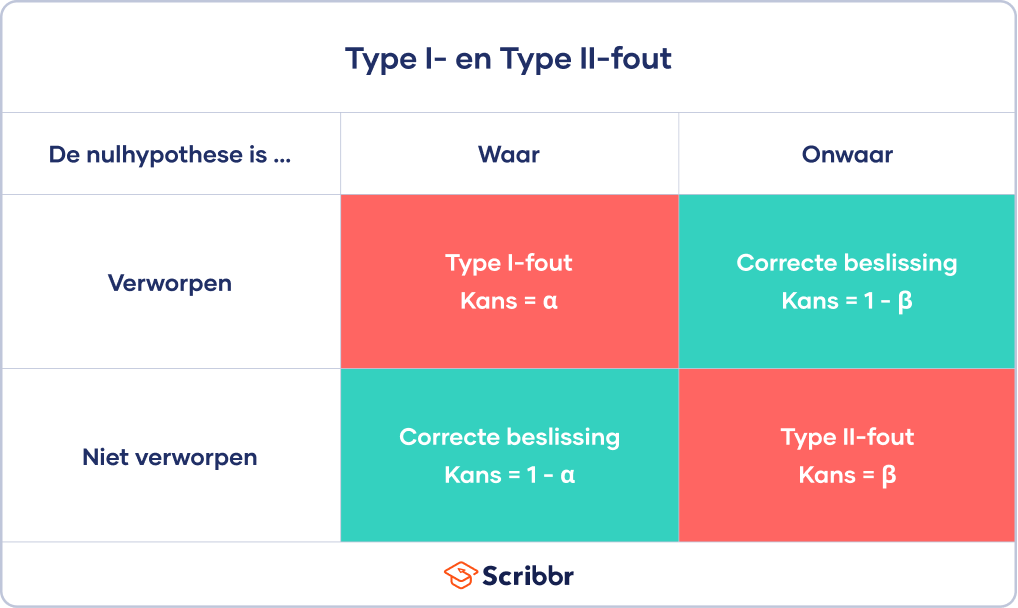
Een Type I-fout is een fout-positieve conclusie (false positive), terwijl een Type II-fout een fout-negatieve conclusie (false negative) is.

Je kunt nooit met 100% zekerheid een conclusie trekken op basis van statistiek, dus het risico op een van deze twee type fouten is onvermijdelijk als je hypothesen toetst.

Het risico dat je een Type I-fout maakt, is gelijk aan het significantieniveau (alfa of α), terwijl het risico op het maken van een Type II-fout gelijk is aan bèta (β). Deze risico’s kunnen worden geminimaliseerd door goed na te denken over je onderzoeksdesign.

Fouten bij statistische conclusies trekken

Hypothesetoetsing is een gestructureerde procedure om onze ideeën over de wereld te onderzoeken met behulp van statistiek. Op basis hiervan beslis je of je data je voorspellingen ondersteunen of juist niet.

Hypothesetoetsing begint met de aanname dat er geen verschil bestaat tussen groepen of dat er geen verband is tussen variabelen in de populatie (de nulhypothese). Verder stel je een alternatieve hypothese op: de voorspelling van een verschil tussen groepen of een relatie tussen variabelen.

Vervolgens beslis je op basis van je data en de resultaten van een statistische toets of de nulhypothese kan worden verworpen of niet. Aangezien deze beslissingen gebaseerd zijn op kansen, is er altijd een risico dat je de verkeerde conclusie trekt.

• Als je resultaten statistisch significant zijn, betekent dit dat het zeer onwaarschijnlijk is dat ze zouden voorkomen als de nulhypothese waar is. In dit geval zou je de nulhypothese verwerpen. In sommige gevallen maak je hiermee een Type I-fout.
• Als je resultaten niet statistisch significant zijn, is er een grote kans dat je de resultaten ook zou vinden als de nulhypothese waar is. Daarom kun je deze niet verwerpen. In sommige gevallen maak je hiermee een Type II-fout.

Wat zijn Type I-fouten?

Een Type I-fout betekent dat de nulhypothese wordt verworpen, terwijl deze eigenlijk waar is. Je concludeert dat resultaten statistisch significant zijn, terwijl ze in werkelijkheid puur door toeval of door niet-gerelateerde factoren zijn veroorzaakt.

Het risico dat je deze fout maakt, is het significantieniveau (alfa of α) dat je zelf kiest aan het begin van je onderzoek. Zo kun je de verkregen p-waarde met dit niveau vergelijken. Op basis daarvan bepaal je of je resultaten significant zijn (p < α).

Het significantieniveau is meestal 0.05 of 5%. Dit betekent dat er slechts een maximale kans van 5% is dat je deze resultaten zou vinden als de nulhypothese echt waar zou zijn.

Als de p-waarde lager is dan het significantieniveau, betekent dit dat je resultaten statistisch significant zijn en dat ze in overeenstemming zijn met de alternatieve hypothese. Als de p-waarde hoger is dan het significantieniveau, zijn de resultaten niet significant.

Om het risico op een Type I-fout te verkleinen, kun je een lager significantieniveau kiezen.

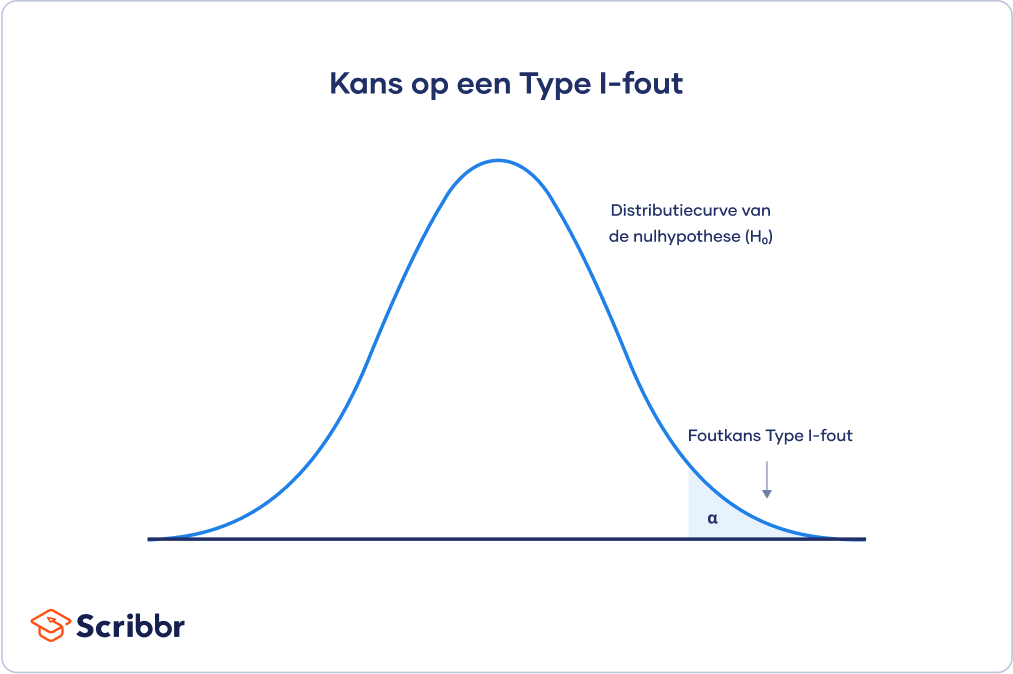
Foutkans Type I-fout

De distributiecurve van de nulhypothese toont de kansen om alle mogelijke resultaten te verkrijgen als:

• Het onderzoek zou worden herhaald met nieuwe steekproeven.
• De nulhypothese waar zou zijn voor de populatie.

Het gearceerde gebied komt overeen met alfa. Dit wordt ook wel het kritieke gebied (critical region) genoemd.

Als je resultaten in het kritieke gebied van deze curve vallen, worden ze als statistisch significant beschouwd en wordt de nulhypothese verworpen. In dat geval is sprake van een false positive, omdat de nulhypothese echt waar is en dus niet verworpen had moeten worden.

Wat zijn Type II-fouten?

Een Type II-fout treedt op als de nulhypothese niet wordt verworpen, terwijl deze eigenlijk wel verworpen had moeten worden. Je concludeert dat er geen effect is, terwijl dit effect in werkelijkheid wel bestaat. Een mogelijke oorzaak voor een Type II-fout is te weinig statistische power (statistical power) om een effect te detecteren.

Power is de mate waarin een toets een effect correct kan detecteren als er daadwerkelijk een effect is. Meestal wordt een power-niveau van 80% of hoger acceptabel gevonden.

Er bestaat een omgekeerd evenredig verband tussen het risico op een Type II-fout en de statistische power van een onderzoek: des te meer statistische power, des te kleiner het risico op een Type II-fout.

Statistische power wordt bepaald door:

• De grootte van het effect: Grotere effecten worden gemakkelijker gedetecteerd.
• Meetfout: Systematische en willekeurige fouten in de data zorgen voor minder power.
• Steekproefomvang: Grotere steekproeven verminderen de steekproeffout (sampling error) en dragen bij aan de power.
• Significantieniveau: Een hoger significantieniveau gaat gepaard met meer power.

Om (indirect) het risico op een Type II-fout te verkleinen, kun je de steekproef vergroten of het significantieniveau verhogen.

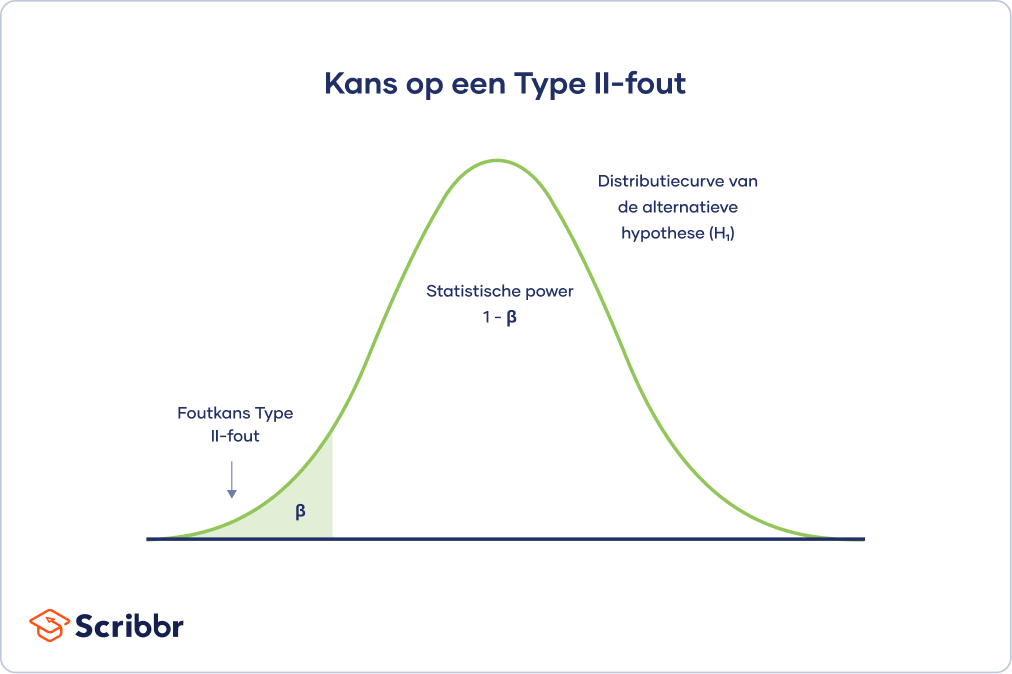
Foutkans Type II-fouten

De distributiecurve voor de alternatieve hypothese toont de kansen om alle mogelijke resultaten te verkrijgen als:

• Het onderzoek zou worden herhaald met nieuwe steekproeven.
• De alternatieve hypothese waar zou zijn voor de populatie.

De foutkans voor Type II-fouten is gelijk aan bèta (β). Deze foutkans wordt gevisualiseerd met behulp van het gearceerde gebied aan de linkerkant. Het resterende gebied onder de curve vertegenwoordigt de statistische power (1 – β).

Door de statistische power van je onderzoek te vergroten, verklein je het risico op een Type II-fout.

Wisselwerking tussen Type I- en Type II-fouten

De foutkansen (error rates) van Type I- en Type II-fouten beïnvloeden elkaar. Dat komt doordat het significantieniveau (de foutkans voor Type I) van invloed is op de statistische power (die een effect heeft op de foutkans voor Type II).

Dit betekent dat er een belangrijke wisselwerking (trade-off) bestaat tussen het risico op Type I- en Type II-fouten:

• Een lager significantieniveau verkleint het risico op Type I-fouten, maar vergroot het risico op Type II-fouten.
• Meer statistische power verkleint het risico op Type II-fouten, maar vergroot het risico op Type I-fouten.

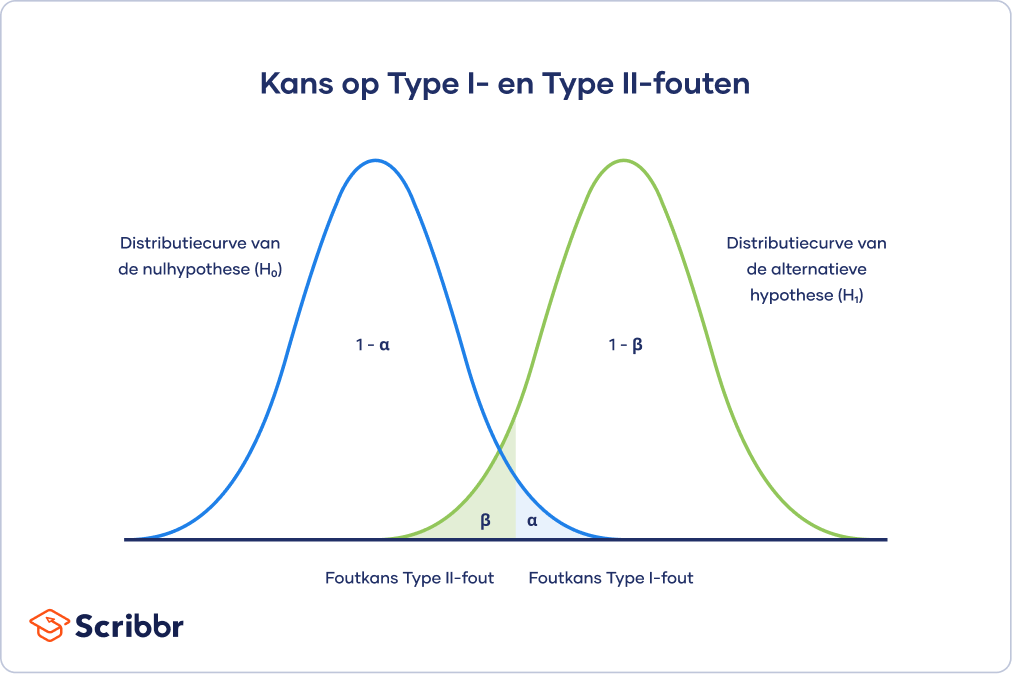
De wisselwerking wordt gevisualiseerd in onderstaande grafiek. Deze laat twee curven zien:

• De verdeling van de nulhypothese toont alle mogelijke resultaten die je zou krijgen als de nulhypothese waar is. Voor alle punten op die verdeling zou de juiste conclusie zijn om de nulhypothese niet te verwerpen.
• De verdeling van de alternatieve hypothese toont alle mogelijke resultaten die je zou krijgen als de alternatieve hypothese waar is. Voor alle punten op die verdeling zou de juiste conclusie zijn om de nulhypothese te verwerpen.

Type I- en Type II-fouten komen voor op de punten waar deze twee verdelingen elkaar overlappen. Het blauw gearceerde gebied komt overeen met alfa (foutkans Type I) en het groen gearceerde gebied komt overeen met bèta (foutkans Type II).

Je keuze voor een foutkans voor Type I-fouten beïnvloedt indirect ook de foutkans voor Type II-fouten.

Het is belangrijk om een balans te vinden tussen het risico op een Type I-fout en het risico op een Type II-fout. Een verlaging van het significantieniveau alfa gaat altijd ten koste van bèta.

Wie helpt jou met nakijken?

Betrouwbare hulptroepen vinden is niet makkelijk...

• Familie
• Vrienden
• Studiegenoten
• Scribbr

We staan altijd voor je klaar

Wat is erger: een Type I-fout of een Type II-fout?

Voor statistici is een Type I-fout meestal erger dan een Type II-fout, maar in de praktijk kunnen beide soorten fouten erger zijn dan de andere soort.

Als je een Type I-fout maakt, verwerp je ten onrechte de nulhypothese. Dit kan bijvoorbeeld leiden tot nieuwe procedures, therapieën of medicijnen waarin beter niet had kunnen worden geïnvesteerd.

In het geval van een Type II-fout heb je de nulhypothese niet verworpen, terwijl deze wel verworpen had moeten worden. Hierdoor kunnen bedrijven of organisaties beslissen om niet in iets te investeren, wat grote gevolgen kan hebben in de praktijk.

Het is belangrijk om onderzoeken te repliceren of reproduceren, zodat verkeerde resultaten en conclusies worden ontdekt en eventuele Type I- of Type II-fouten geen ernstige gevolgen hebben.

Veelgestelde vragen

Wat zijn Type I-fouten en Type II-fouten?

Een Type I-fout is een fout-positieve conclusie (false positive), terwijl een Type II-fout een fout-negatieve conclusie (false negative) is.

• Als je een Type I-fout maakt, verwerp je de nulhypothese ten onrechte.
• Als je een Type II-fout maakt, verwerp je de nulhypothese ten onrechte niet.

Hoe verklein je het risico op een Type I-fout?

Het risico op een Type I-fout is gelijk aan het significantieniveau dat je kiest voor je onderzoek. Je vergelijkt de p-waarde met dit niveau om te bepalen of je resultaten statistisch significant zijn.

Het significantieniveau is meestal 0.05 of 5%. Dit betekent dat er een kans van 5% is dat de gevonden resultaten zouden voorkomen als de nulhypothese daadwerkelijk waar zou zijn.

Om het risico op een Type I-fout te verkleinen, verlaag je het significantieniveau alfa. Hiermee vergroot je wel het risico op een Type II-fout.

Hoe verklein je het risico op een Type II-fout?

Er bestaat een omgekeerd evenredig verband tussen het risico op een Type II-fout en de statistische power van een onderzoek. De power is de mate waarin een toets een daadwerkelijk bestaand effect correct kan detecteren.

Om het risico op een Type II-fout (indirect) te verkleinen, kun je de steekproef vergroten of het significantieniveau verhogen, omdat je zo de statistische power vergroot.

Wat is statistische significantie?

Statistische significantie is een term die door onderzoekers wordt gebruikt om aan te geven dat het onwaarschijnlijk is dat hun resultaten op toeval gebaseerd zijn. Significantie wordt meestal aangeduid met een p-waarde (overschrijdingskans).

Statistische significantie is enigszins willekeurig, omdat je zelf de drempelwaarde (alfa) kiest. De meest voorkomende drempel is p < 0.05, wat betekent dat de kans 5% is dat de resultaten worden gevonden terwijl de nulhypothese waar is. Een andere drempel die vaak wordt gekozen is p < 0.01.

Als de p-waarde lager is dan de gekozen alfa-waarde, mag je stellen dat het resultaat van de toets statistisch significant is.

Wat is statistische power (statistical power)?

Statistische power (statistical power) verwijst naar de waarschijnlijkheid dat een hypothesetoets een echt effect vaststelt als dat effect er is. Dit noem je ook wel het onderscheidend vermogen. Een toets met veel statistische power is beter in staat een Type II-fout (false negative) te voorkomen.

Als je onderzoek onvoldoende power heeft, kan het voorkomen dat je geen statistisch significant resultaat vindt, zelfs als dit wel aanwezig is en praktische relevantie heeft. Hierdoor zou je ten onrechte de nulhypothese behouden.