Centrummaten: Modus, mediaan en gemiddelde | Met voorbeelden
Centrummaten (measures of central tendency) helpen je het midden of gemiddelde van een dataset te vinden. De drie meest voorkomende centrummaten zijn de modus (mode), mediaan (median) en het gemiddelde (mean).
- Modus: de waarde die het vaakst voorkomt.
- Mediaan: de middelste waarde als je de dataset van kleinste naar grootste waarde rangschikt.
- Gemiddelde: de som van alle waarden, gedeeld door het totale aantal waarden.
Als je beschrijvende statistieken gebruikt om je data samen te vatten, kijk je niet alleen naar de centrale tendens (central tendency), maar ook naar de verdeling en spreiding of variabiliteit van je dataset.
Verdelingen en centrale tendens
Een dataset is een verdeling van een n aantal scores of waarden.
Normale verdeling
Bij een normale verdeling zijn de gegevens symmetrisch verdeeld zonder scheeftrekking. De meeste waarden clusteren rond een centraal gebied, waarbij het aantal waarden afneemt naarmate ze verder verwijderd zijn van het midden. Het gemiddelde, de modus en de mediaan zijn precies hetzelfde in een normale verdeling.
Een histogram van je data toont de frequentie voor iedere respons. Als je naar het voorbeeld kijkt, zie je dat dat de data normaal verdeeld zijn.
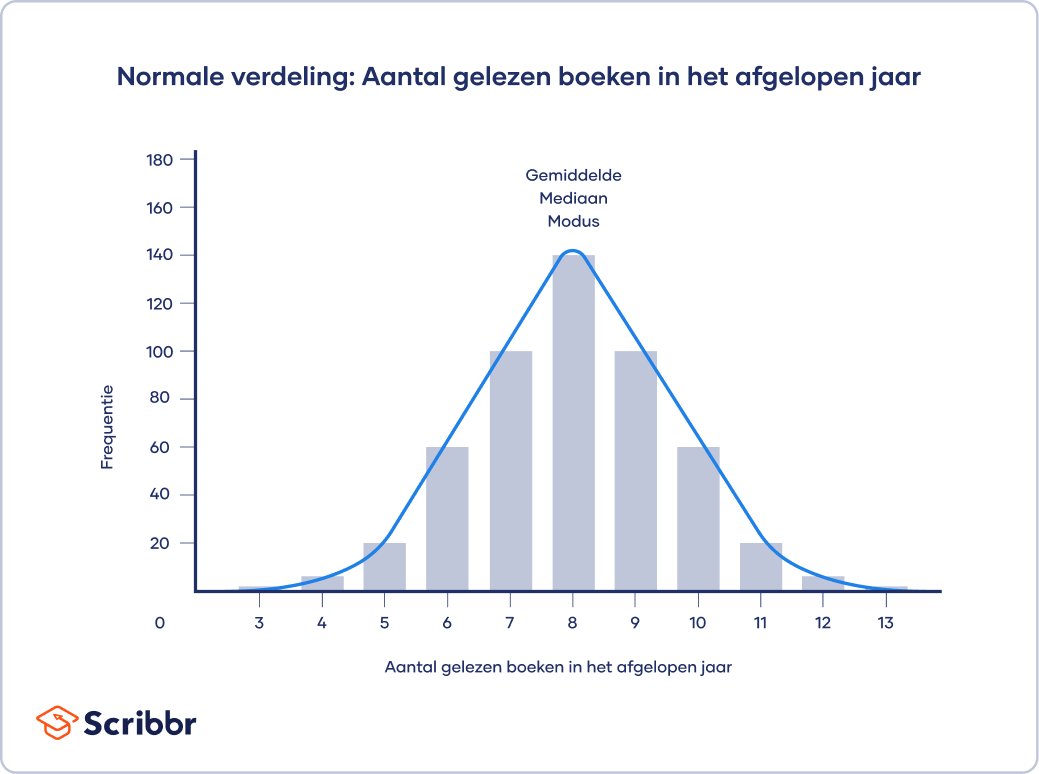
De modus, mediaan en het gemiddelde zijn hetzelfde. De centrale tendens van deze dataset is 8.
Scheve verdelingen
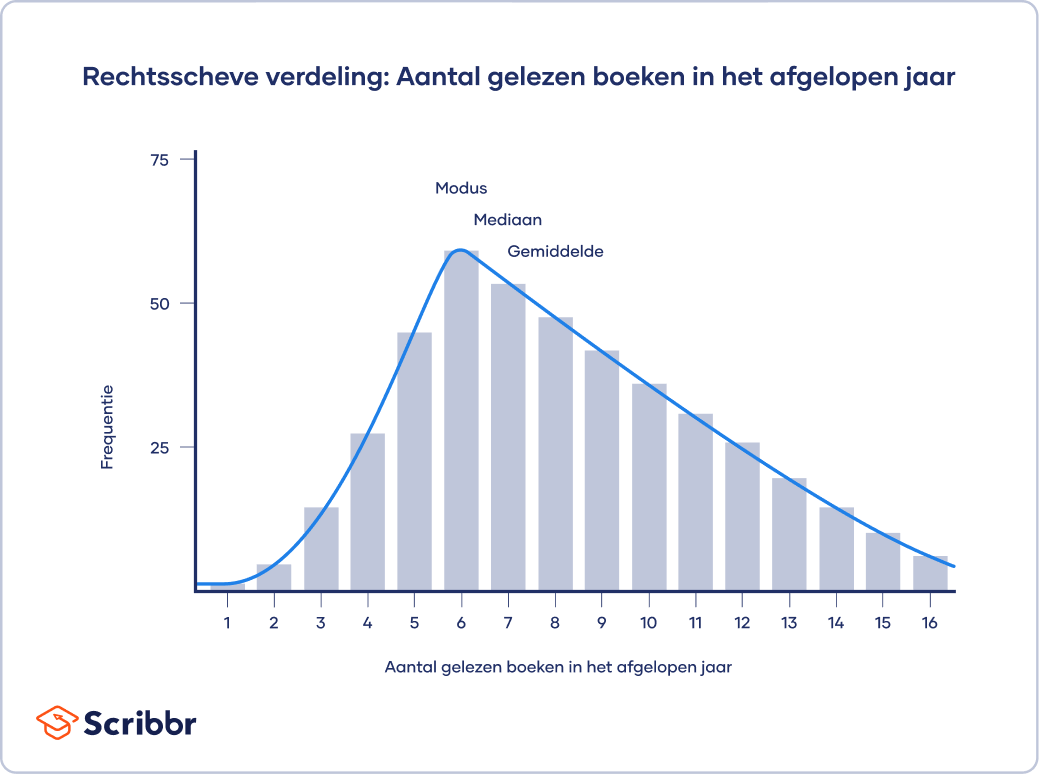
Bij scheve verdelingen (skewed distributions) bevinden meer waarden zich aan de ene kant van het centrum dan aan de andere kant. Het gemiddelde, de mediaan en de modus verschillen allemaal van elkaar. De ene kant heeft een meer gespreide, plattere en langere staart met minder scores aan het ene uiteinde dan aan het andere.
In een positief-scheve of rechtsscheve verdeling is er een cluster van lagere scores en een platte staart aan de rechterkant. In een negatief-scheve of linksscheve verdeling is er een cluster van hogere scores en een platte staart aan de linkerkant.
Het voorbeeld laat zien dat de verdeling rechtsscheef is, waarbij de frequentiepiek zichtbaar is aan de linkerkant. Bij een positief-scheve verdeling is de modus kleiner dan de mediaan en de mediaan weer kleiner dan het gemiddelde: modus < mediaan < gemiddelde.
Lees waarom zo veel studenten Scribbr inschakelen
Modus
De modus is de waarde die het vaakst voorkomt in de dataset. Je kunt geen modus, één modus of meer dan één modus hebben.
Om de modus te vinden, sorteer je de waarden in je dataset (categorisch of van kleinste naar grootste waarde), en selecteer je de antwoordoptie die het vaakst is gekozen.
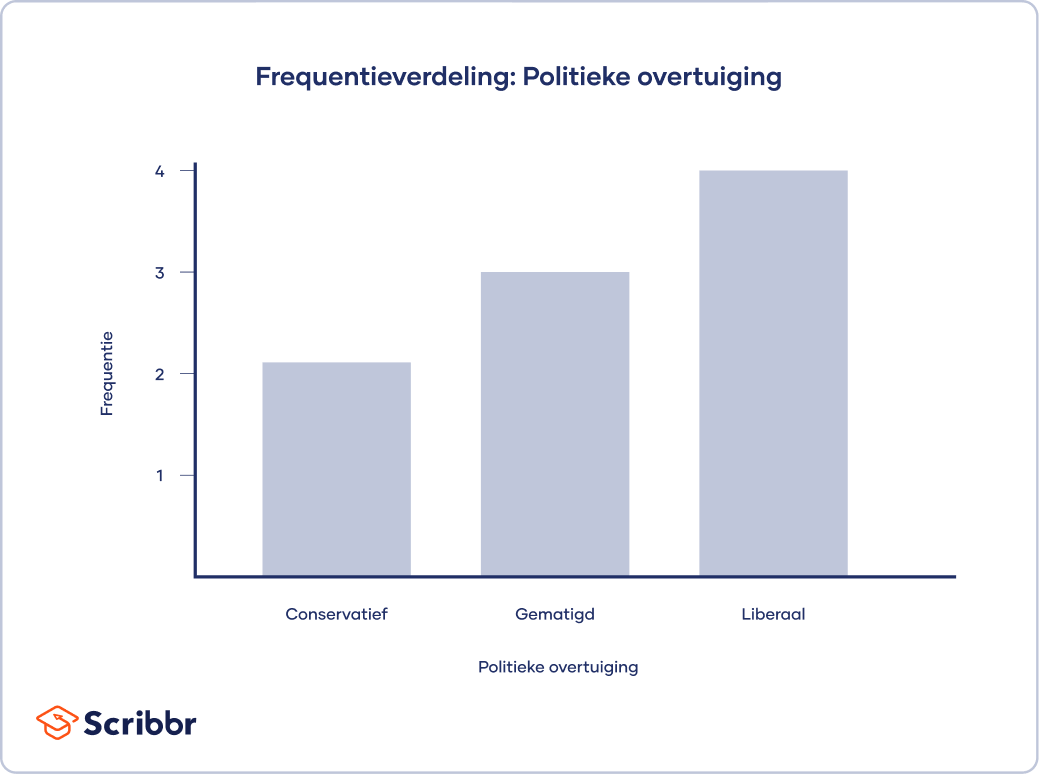
Om de modus te vinden, sorteer je de data op categorie en bepaal je welk antwoord het vaakst werd gekozen. Om dit proces makkelijker te maken, kun je een frequentietabel opvragen, waarbij de waarden voor iedere categorie automatisch worden opgeteld.
| Politieke overtuiging | Frequentie |
|---|---|
| Conservatief | 2 |
| Gematigd | 3 |
| Liberaal | 4 |
Modus: Liberaal
Je kunt de modus snel vinden in een staafdiagram, omdat de modus de waarde is met de hoogste staaf.
Wanneer gebruik je de modus?
De modus is het meest van toepassing op nominale data. Nominale data kunnen worden gecategoriseerd in elkaar uitsluitende categorieën (ieder antwoord kan maar in één categorie vallen), dus de modus is de meest populaire categorie.
Voor continue variabelen of variabelen van rationiveau is de modus soms niet nuttig om inzicht te krijgen in de centrale tendens. Er zijn namelijk veel meer mogelijke antwoordopties dan op een nominaal of ordinaal meetniveau.
Bij een onderzoek naar reactietijden is het bijvoorbeeld onwaarschijnlijk dat meerdere mensen exact dezelfde reactietijd hebben. Hierdoor kun je geen modus vinden.
| Participant | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| Reactietijd (milliseconden) | 267 | 345 | 421 | 324 | 401 | 312 | 382 | 298 | 303 |
In deze dataset kun je geen modus vinden, omdat alle waarden maar één keer voorkomen.
Mediaan
De mediaan is de waarde in het midden van een dataset als je de waarden in volgorde hebt gezet van laag naar hoog.
| Participant | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| Snelheid | Gemiddeld | Langzaam | Snel | Snel | Gemiddeld | Snel | Langzaam |
Om de mediaan te vinden, zet je eerst alle waarden van laag naar hoog. Vervolgens zoek je de waarde in het midden. In dit geval is dat de waarde op de vierde positie.
| Gesorteerde dataset | Langzaam | Langzaam | Gemiddeld | Gemiddeld | Snel | Snel | Snel |
|---|
Mediaan: Gemiddeld
In grotere datasets is het makkelijker om formules te gebruiken om de middelste waarde te vinden. Je kunt de mediaan op verschillende manieren vinden, afhankelijk van het totale aantal waarden (even aantal of oneven aantal).
Mediaan van een dataset met een oneven aantal waarden
Voor een dataset met een oneven aantal waarden zoek je de waarde op positie (n+1)/2. In deze formule is n het aantal waarden in de dataset.
| Reactietijd (milliseconden) | 287 | 298 | 345 | 365 | 380 |
|---|
Je berekent de middelste positie met de formule 
, waarbij n = 5.
Dat betekent dat de mediaan de derde waarde in je gesorteerde dataset is.
Mediaan: 345 milliseconden
Mediaan van een dataset met een even aantal waarden
Voor een dataset met een even aantal waarden, zoek je de twee middelste waarden in de dataset, namelijk die op positie 
en 
. Vervolgens bepaal je het gemiddelde van die twee waarden om je mediaan te vinden.
| Reactietijd (milliseconden) | 287 | 298 | 345 | 357 | 365 | 380 |
|---|
De middelste posities worden bepaald met formules en , waarbij n = 6.
Dat betekent dat de middelste waarden op de derde positie (345) en de vierde positie (357) staan.
Om de mediaan te bepalen, bereken je het gemiddelde van de twee waarden door ze bij elkaar op te tellen en door 2 te delen.
Mediaan: 351 milliseconden
Gemiddelde
Het rekenkundig gemiddelde van een dataset is de som van alle waarden, gedeeld door het totale aantal waarden. Dit is de meest gebruikte centrummaat, omdat je alle waarden gebruikt in de berekening.
| Participant | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| Reactietijd (milliseconden) | 287 | 345 | 365 | 298 | 380 |
Eerst tel je alle waarden bij elkaar op:
Vervolgens bereken je het gemiddelde met de formule 
. De dataset bevat 5 waarden, dus n = 5.
Gemiddelde: 335 milliseconden
Het effect van uitbijters op het gemiddelde
Uitbijters (ook uitschieters of outliers genoemd) kunnen het gemiddelde sterk verlagen of verhogen als je ze opneemt in de berekening. Aangezien je alle waarden gebruikt om het gemiddelde te berekenen, kan deze centrummaat sterk worden beïnvloed door extreme uitbijters. Een uitbijter is een waarde die significant verschilt van andere waarden in de dataset.
| Participant | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| Reactietijd (milliseconden) | 832 | 345 | 365 | 298 | 380 |
Het gemiddelde (
)wordt veel hoger vanwege de uitbijter, ook al zijn de andere waarden in de dataset hetzelfde gebleven.
Gemiddelde: 444 milliseconden
Populatiegemiddelde versus steekproefgemiddelde
Een dataset bevat waarden uit een steekproef of een populatie. Een populatie is de gehele groep die je wilt onderzoeken, terwijl een steekproef slechts een subset van die populatie is.
Steekproefdata kunnen je helpen om uitspraken te doen over de populatie (schattingen), maar alleen data van de gehele populatie kunnen een volledig beeld geven.
Bij statistiek gebruik je andere symbolen en formules voor steekproefgemiddelden en populatiegemiddelden. De procedures om de twee soorten gemiddelden te berekenen zijn wel hetzelfde.
Het steekproefgemiddelde wordt uitgedrukt met het symbool M of x̄. Je gebruikt de volgende formule om het gemiddelde van een steekproef te berekenen:
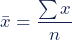
- x̄: steekproefgemiddelde
- ⅀x: som van alle waarden in de steekproef-dataset
- n: aantal waarden in de steekproef-dataset
Het populatiegemiddelde wordt uitgedrukt met het symbool μ (Griekse letter mu). Je gebruikt de volgende formule om het gemiddelde van een populatie te berekenen:
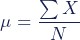
- μ: populatiegemiddelde
- ⅀X: som van alle waarden in de populatie-dataset
- N: aantal waarden in de populatie-dataset
Wanneer gebruik je het gemiddelde, de mediaan of de modus?
De drie belangrijkste centrummaten kunnen het beste in combinatie met elkaar worden gebruikt, omdat ze aanvullende sterke punten en beperkingen hebben. Soms kun je er maar één of twee gebruiken, afhankelijk van het meetniveau van de variabele.
- De modus kan voor ieder meetniveau worden gebruikt, maar is het meest zinvol voor nominale en ordinale niveaus.
- De mediaan kan alleen worden gebruikt voor data die op een logische manier kunnen worden geordend. Daarom is deze maat alleen geschikt voor ordinale, interval- en ratiodata.
- Het gemiddelde kan alleen worden gebruikt voor interval- en ratiodata, omdat je voor deze maat gelijke intervallen tussen aangrenzende scores of waarden nodig hebt.
| Meetniveau | Voorbeelden | Centrummaat |
|---|---|---|
| Nominaal |
|
|
| Ordinaal |
|
|
| Interval en ratio |
|
|
Bij de keuze voor een of meerdere centrummaten moet je ook rekening houden met de verdeling van je dataset.
Voor normaal verdeelde data kun je alle drie de centrummaten gebruiken. In dit geval hebben ze allemaal dezelfde waarde (gemiddelde = mediaan = modus).
Bij scheve verdelingen kun je de het beste de mediaan gebruiken, omdat deze niet wordt beïnvloed door extreme uitbijters of een asymmetrische verdeling. Het gemiddelde en de modus kunnen variëren bij scheve verdelingen.
Veelgestelde vragen
- Wat zijn centrummaten (measures of central tendency)?
-
Centrummaten (measures of central tendency) helpen je het centrum of midden van een dataset te vinden.
De drie meest gebruikte centrummaten zijn het gemiddelde, de mediaan en de modus.
- De modus is de waarde die het vaakst voorkomt
- De mediaan is de middelste waarde als je de dataset van kleinste naar grootste waarde rangschikt.
- Het gemiddelde is de som van alle waarden, gedeeld door het totale aantal waarden.
- Welke centrummaten kan ik gebruiken met mijn data?
-
Welke centrummaten je kunt gebruiken, is afhankelijk van het meetniveau en de verdeling van je data.
- Voor nominale data, kun je alleen de modus gebruiken om de meest voorkomende waarde te vinden.
- Voor ordinale data kun je zowel de modus en de mediaan gebruiken.
- Voor interval- of ratiodata kun je, naast de modus en mediaan, ook het gemiddelde gebruiken.
Ook moet je op de verdeling van je data letten. Voor normaal verdeelde data kun je alle drie de centrummaten gebruiken, maar bij scheve verdelingen is de mediaan de beste keuze.
- Wat zijn de vier meetniveaus?
-
Meetniveaus laten zien hoe precies variabelen worden gemeten. Er zijn vier meetniveaus (of meetschalen) die van laag naar hoog kunnen worden gerangschikt.
- Nominaal: De data kunnen alleen worden gecategoriseerd (geen rangorde).
- Ordinaal: De data kunnen worden gecategoriseerd en gerangschikt.
- Interval: De data kunnen worden gecategoriseerd en gerangschikt en er zijn gelijke intervallen tussen de categorieën.
- Ratio: De data kunnen worden gecategoriseerd en gerangschikt, de intervallen zijn gelijk, en er is een absoluut of betekenisvol nulpunt.
Citeer dit Scribbr-artikel
Als je naar deze bron wilt verwijzen, kun je de bronvermelding kopiëren of op “Citeer dit Scribbr-artikel” klikken om de bronvermelding automatisch toe te voegen aan onze gratis Bronnengenerator.
Merkus, J. (2021, 21 oktober). Centrummaten: Modus, mediaan en gemiddelde | Met voorbeelden. Scribbr. Geraadpleegd op 23 november 2024, van https://www.scribbr.nl/statistiek/centrummaten/
